薬剤師のプログラミング学習日記

プログラミングやコンピュータに関する記事を書いていきます

トップ > 薬物動態 > バンコマイシンの血中濃度データに2-コンパートメントモデルを当てはめる

バンコマイシンの血中濃度データに2-コンパートメントモデルを当てはめる

薬物動態

点滴静注したバンコマイシン*1の血中濃度データが得られたとして、これを2-コンパートメントモデルに当てはめ、薬物動態パラメータを求めてみます。

f:id:enokisaute:20200307140939p:plain

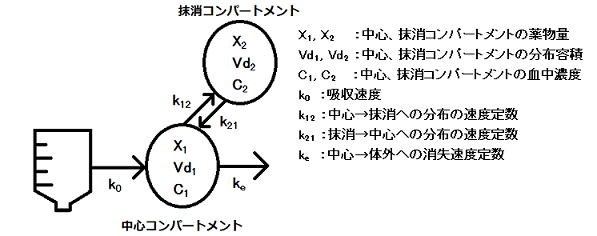
2-コンパートメント点滴静注モデル

0次速度の吸収過程を持つ2-コンパートメントモデルの薬物量の変化は次のような２つの微分方程式で記述できます。

f:id:enokisaute:20200307141215p:plain

\frac{dX_1}{dt} = k_0 + k_{21} \cdot X_2 - k_{12} \cdot X_1 - k_e \cdot X_1

\frac{dX_2}{dt} = k_{12} \cdot X_1 - k_{21} \cdot X_2

この連立微分方程式を解くと、以下の血中濃度推移を求める式が得られます。

C_1 = A(1 - e^{-αt}) + B(1 - e^{-βt})~~~~~~(α>β)~~~~~~(1)


ここで、A, B, α, βはそれぞれ

A = \frac{k_0(k_{21} - α)}{Vd_1 \cdot α(β - α)}~, ~~~B = \frac{k_0(k_{21} - β)}{Vd_1 \cdot β(α - β)}

α = \frac{1}{2}(k_{12} + k_{21} + k_e + z)~, ~~~β = \frac{1}{2}(k_{12} + k_{21} + k_e - z)

z = \sqrt{(k_{12} + k_{21} + k_e)^2 - 4 \cdot k_{21} \cdot k_e}

です。また、これらの関係からk_{12}, k_{21}, k_eを求めることもできます。

ここで、点滴終了時を\ T_{\rm inf}\ とすると(1)の式は\ t≤T_{\rm inf}\ でした。
では次に、点滴終了後（\ t＞T_{\rm inf}\ ）の血中濃度推移を求める式ですが、次のように表すことができます。

C_1 = A(1 - e^{-αT_{\rm inf}}) \cdot e^{-α(t - T_{\rm inf})} + B(1 - e^{-βT_{\rm inf}}) \cdot e^{-β(t - T_{\rm inf})}~~~~~~(2)

式を整理すると、

C_1 = A( e^{-α(t - T_{\rm inf})}- e^{-αt}) + B( e^{-β(t - T_{\rm inf})} - e^{-βt})~~~~~~(3)

となります。
これらの式を使って薬物動態パラメータを求めていきます。

残差法で回帰直線のパラメータを求める

それでは、血中濃度のデータをこのモデルに当てはめ、A, B, α, βを求めていきたいと思います。その方法については、こちらのページを参考に考えてみました。

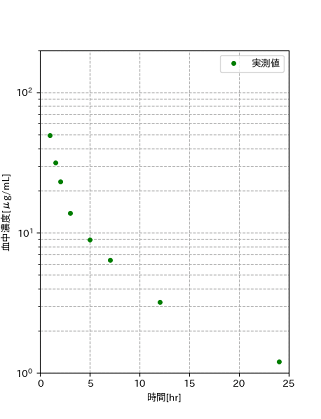
「血中濃度データに1-コンパートメント急速静注モデルを当てはめる」でやったように、血中濃度を対数変換し、片対数プロットして線形回帰しますが、2-コンパートメントモデルの場合は下図のように1つの直線ではなく、2つの直線が組み合わさっているような推移を示します。

# VCM 1.0gを1時間で点滴静注したときの8点の血中濃度データ
t = np.array([1.0, 1.5, 2.0, 3.0, 5.0, 7.0, 12.0, 24.0])   # 時間
c = np.array([49.5, 31.6, 23.3, 13.8, 8.9, 6.4, 3.2, 1.2]) # 血中濃度

f:id:enokisaute:20200307141026p:plain

まず、上の(2)式を次のように書き直します。

C_1 = P \cdot e^{-α(t - T_{\rm inf})} + Q \cdot e^{-β(t - T_{\rm inf})}~~~~~~(4)

このとき、tが大きい部分ではα＞βであるため前のPの項は無視して、次のような近似式で表すことができます。

C_1 ≒ Q \cdot e^{-β(t - T_{\rm inf})}

この状態では組織への分布が完了し、コンパートメント間で平衡状態となっており、これをβ相（消失相）と言います。その前の、薬が中心コンパートメントから各組織への分布が完了するまでがα相（分布相）です。
次に、この式を常用対数表示にすると、

log_{10}C_1 = log_{10}Q - \frac{β}{2.303}(t - T_{\rm inf})

となります。あとは、測定データにこの回帰直線を当てはめ傾きβと切片Qを求めます。
次はα相です。上の(4)式を変形して

C_1 - Q \cdot e^{-β(t - T_{\rm inf})} = P \cdot e^{-α(t - T_{\rm inf})}

log_{10}(C_1 - Q \cdot e^{-β(t - T_{\rm inf})}) = log_{10}P - \frac{α}{2.303}(t - T_{\rm inf})~~~~~~(5)

となります。この左辺の真数部分は『測定した血中濃度の値 －各時間におけるβ相の直線上の値』を意味します。

これでα相とβ相の２つの直線の式が得られました。
では実際にコードを書いていきます。

import numpy as np
import matplotlib.pyplot as plt
 
x0 = 1000    # 投与量(mg)
T = 1.0      # 点滴時間(hr)
 
# VCM 1.0gを1時間で点滴静注したときの8点の血中濃度データ
t = np.array([1.0, 1.5, 2.0, 3.0, 5.0, 7.0, 12.0, 24.0])
c = np.array([49.5, 31.6, 23.3, 13.8, 8.9, 6.4, 3.2, 1.2])
 
 
# 最小二乗法により回帰直線のintercept, slopeを返す
def least_squares_method(xdata, ydata):
    X = np.zeros((len(xdata), 2), float)  # データ数×2列の行列を作る
    X[:, 0] = 1
    X[:, 1] = xdata
    logy = np.log10(ydata)  # 血中濃度の常用対数をとる
    (theta, residuals, rank, s) = np.linalg.lstsq(X, logy, rcond=None)
    return theta[0], theta[1]
 
 
# α・β相の傾きと切片を求める
# 後半の4点をβ相とする
intercept_q, slope_b = least_squares_method(t[4:8] - T, c[4:8])
 
# 最初の4点の実測値 - 消失相(β相)の外挿した直線上の値との差を求める.
c_diff = [c_data - pow(10, intercept_q + slope_b * (x - T))
          for (x, c_data) in zip(t[:4], c[:4])]
 
# 前半の４点をα相とする
intercept_p, slope_a = least_squares_method(t[:4] - T, c_diff)
 
# 傾きからalpha, betaを求める
alpha = slope_a * -2.303                  
beta = slope_b * -2.303
# 切片からA, Bを求める
A = 10 ** intercept_p / (1 - np.exp(-alpha * T))
B = 10 ** intercept_q / (1 - np.exp(-beta * T))
 
print('A: {}, alpha: {}'.format(A, alpha))
print('B: {}, beta: {}'.format(B, beta))

最小二乗法により回帰直線の切片と傾きを求めるやり方は「血中濃度データに1-コンパートメント急速静注モデルを当てはめる」でやったのと同じですが、関数にしています。
まずβ相ですが、t, cともに後半の４点を[4:8]のようにスライスを使って指定し、関数に渡しています。
次のα相ですが、まず(5)式の左辺の真数の部分です。

c_diff = [c_data - pow(10, intercept_q + slope_b * (x - T))
          for (x, c_data) in zip(t[:4], c[:4])]


数式のQ \cdot e^{-β(t - T_{\rm inf})}は、先に求めた切片と傾きからpow()を使って10のべき乗として計算しています。そしてここで求めたc_diffとtの前半の４点でα相の傾きと切片を求めます。*2

これでα、β相の２つの直線の傾きと切片がわかったので、あとはA、B、α、βを求めるだけです。私の環境では、次のような値になりました。

A: 55.17473179954318, alpha: 1.0960384175663902
B: 121.92396189775874, beta: 0.1027524118430043

このA、B、α、βを(3)の式に入れてプロットしたものが、冒頭のグラフ右側になります。

非線形最小二乗法によるフィッティング

最小二乗法では、測定されたデータにうまくフィットするような関数のパラメータ（係数）を求めますが、コンパートメントモデルのような複雑な関数の場合はパラメータを求めるための方程式を解析的に解くことができず、反復計算によって求めることになります。
この反復計算を始める際には、パラメータの値としてある程度真値に近い初期値を指定してやる必要があります。ここまでのところで、対数変換したデータに回帰直線を当てはめ、2-コンパートメント点滴静注モデルの関数のパラメータを求めました。
ここではこのパラメータの値を初期値として、scipyの関数を用いた非線形最小二乗法でのフィッティングをしてみます。

from scipy import optimize
 
# VCM 1.0gを1時間で点滴静注したときの8点の血中濃度データ
t = np.array([1.0, 1.5, 2.0, 3.0, 5.0, 7.0, 12.0, 24.0])
c = np.array([49.5, 31.6, 23.3, 13.8, 8.9, 6.4, 3.2, 1.2])
 
# A: 55.17473179954318, alpha: 1.0960384175663902
# B: 121.92396189775874, beta: 0.1027524118430043

# 先に求めた値を初期値として使う
init_param = [A, alpha, B, beta]
 
# パラメータをフィッティングしたい関数を定義する
def func(param, t, c, T=1.0):
    A = param[0]
    alpha = param[1]
    B = param[2]
    beta = param[3]
    return A * (np.exp(-alpha * (t-T)) - np.exp(-alpha * t)) \
        + B * (np.exp(-beta * (t-T)) - np.exp(-beta * t)) - c
 
result_param = optimize.leastsq(func, init_param, args=(t, c))

コードは続きとなりますので、既にA、B、α、βには先に求めた値が入っているものとします。
まず一行目はモジュールのインポートです。次に、初期値として各パラメータの値をリストにした後、点滴終了後の式(3)をdef funcとして定義しています。ここは方程式が=0となるように記述するので、

A( e^{-α(t - T_{\rm inf})}- e^{-αt}) + B( e^{-β(t - T_{\rm inf})} - e^{-βt}) - C

と書いています。
そして一番下がleastsq関数ですが、後ろの引数args=()で測定データを渡しています。このleastsqという関数はLevenerg-Marquardt 法というアルゴリズムを使用しており、”初期値が正解から離れている場合は収束が遅くなるが、安定して収束する方法”とのこと。

そしてA、α、B、βは次のような値になりました。

[ 48.51929027   1.25873556 116.69010502   0.13384337]

これらのパラメータを使い、点滴中を(1)式、点滴終了後を(3)式で血中濃度推移をプロットすると下の図のようになります。

C_1 = A(1 - e^{-αt}) + B(1 - e^{-βt})~~~~~~(α>β)~~~~~~~~~~~~~~(1)

C_1 = A( e^{-α(t - T_{\rm inf})}- e^{-αt}) + B( e^{-β(t - T_{\rm inf})} - e^{-βt})~~~~~~(3)

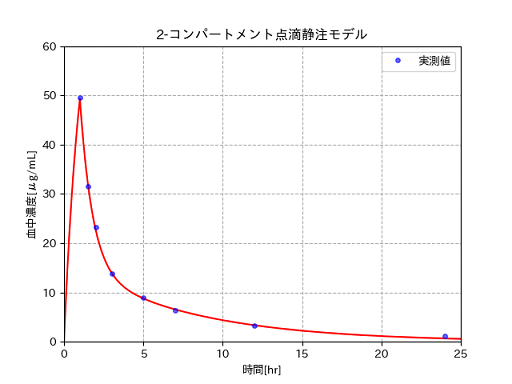
f:id:enokisaute:20200307141435p:plain

ちなみに、同じscipyのcurve_fitを使うと、今回のケースでは初期値がなくてもほぼ同様にフィッティングすることができます（leastsqの場合とはA、Bの値が逆になっていて、数値も微妙に違いますが）。内部的にはleastsqを呼び出しているようなのですが、初期値がなくても良いというのはより使いやすそう。

# モデル関数. 第一引数は独立変数, 第二引数以降はフィッティングパラメータ
def func2(t, A, B, alpha, beta):
    return A * (np.exp(-alpha * (t-1.0)) - np.exp(-alpha * t)) \
        + B * (np.exp(-beta * (t-1.0)) - np.exp(-beta * t))
 
# expがオーバーフローする等の警告が出るが結果は出るのでとりあえず無視.
import warnings
warnings.filterwarnings('ignore')
result, cov = optimize.curve_fit(func2, t, c) 
print(result)



薬物動態パラメータを求める

ページ冒頭で示したA、B、α、βの式からk_{21}, k_e, k_{12}, Vd_1を求める式を導くことができます。
A、Bの式を変形して

A \cdot α(α - β) \cdot Vd_1 + k_0 \cdot k_{21} = k_0 \cdot α
B \cdot α(α - β) \cdot Vd_1 - k_0 \cdot k_{21} = -k_0 \cdot β

これをVd_1, \ k_{21}が未知数の2元連立1次方程式として解くと、

\displaystyle{ Vd_1 = \frac{k_0}{Aα + Bβ}, \ \ k_{21} = \frac{Aαβ + Bαβ}{Aα + Bβ}}

となります。k_e, \ k_{12}は式変形するだけです。

\displaystyle{ k_e = \frac{αβ}{k_{21}}, \ k_{12} = α + β - k_{21} - k_e}

また、\rm{AUC}_{0-∞}は０～T_{inf}（点滴終了まで）とT_{inf}～∞のAUCの和*3で求められ、以下のようになります（×T_{inf}となっていますが、A、Bに1/T_{inf}が入っているのでT_{inf}は消えます）。

AUC_{0-∞} = (A + B) \cdot T_{inf}

これは、「1-コンパートメント点滴静注繰り返し投与ー最高・最低血中濃度とAUCー」で見たように、繰り返し投与時の投与間隔のAUCと同じであり、また２-コンパートメント急速静注モデルでのAUCとも同じになります。


定常状態での分布容積V_{ss}についてみてみます。定常状態では中心・抹消コンパートメント間での薬物の行き来は見かけ上なくなり、両コンパートメントの薬物濃度は等しいと考えると、Vd_2は以下の式で表されます。

Vd_2 = \frac{k_{12}}{k_{21}} \cdot Vd_1

V_{ss}はVd_1とVd_2の和であるため、

V_{ss} = Vd_1 + Vd_2 = (1 + \frac{k_{12}}{k_{21}}) \cdot Vd_1


では、コードで書いてみます。

k21 = (A * alpha * beta + B * alpha * beta) / (A * alpha + B * beta)
ke = (alpha * beta) / k21
k12 = alpha + beta - k21 - ke
Vd1 = x0 / T / (A * alpha + B * beta)
 
print('AUC(μg・hr/mL): ', (A + B) * T)
print('t_half(hr)(β相): ', np.log(2) / beta)
print('ke(hr^-1): ', ke)
print('k12(hr^-1): ', k12)
print('k21(hr^-1): ', k21)
print('CL(mL/min):', ke * Vd1 * 1000 / 60)
print('Vd1(L): ', Vd1)
print('Vss(L): ', Vd1 * (1 + k12 / k21))


結果は、次のようになりました。

AUC(μg・hr/mL):  165.20939529041303
t_half(hr)(β相):  5.1787934102458175
ke(hr^-1):  0.4642057638710173
k12(hr^-1):  0.5654448622472403
k21(hr^-1):  0.36292831194850056
CL(mL/min): 100.88207536483745
Vd1(L):  13.039313582439902
Vss(L):  33.354655840630905

インタビューフォーム記載の値と比べてみました。
単位は上と同じです。

投与量(g) AUC_{0-∞} T_{1/2} k_{el} k_{12} k_{21} CL V_c V
1.0 166 5.23 0.52 0.72 0.41 105.1 12.5 33.2

どれも微妙に違いますね・・。まあこんなもんかな、というかんじでしょうか。*4

参考

  • 徹底解説　薬物動態の数学ー微積分と対数、非線形ー
  • はじめての薬物速度論-薬物動態の基礎

最後に、コード全文を載せておきます。

import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
 
x0 = 1000    # 投与量(mg)
T = 1.0      # 点滴時間(hr)
 
# VCM 1.0gを1時間で点滴静注したときの8点の血中濃度データ
t = np.array([1.0, 1.5, 2.0, 3.0, 5.0, 7.0, 12.0, 24.0])
c = np.array([49.5, 31.6, 23.3, 13.8, 8.9, 6.4, 3.2, 1.2])
 
 
# 最小二乗法により回帰直線のintercept, slopeを返す
def least_squares_method(xdata, ydata):
    X = np.zeros((len(xdata), 2), float)  # データ数×2列の行列を作る
    X[:, 0] = 1
    X[:, 1] = xdata
    logy = np.log10(ydata)  # 血中濃度の常用対数をとる
    (theta, residuals, rank, s) = np.linalg.lstsq(X, logy, rcond=None)
    return theta[0], theta[1]
 
 
# α・β相の傾きと切片を求める
# 後半の4点をβ相とする
intercept_q, slope_b = least_squares_method(t[4:8] - T, c[4:8])
 
# 最初の4点の実測値 - 消失相(β相)の外挿した直線上の値との差を求める.
c_diff = [c_data - pow(10, intercept_q + slope_b * (x - T))
          for (x, c_data) in zip(t[:4], c[:4])]
 
# 前半の４点をα相とする
intercept_p, slope_a = least_squares_method(t[:4] - T, c_diff)
 
# 傾きからalpha, betaを求める
alpha = slope_a * -2.303
beta = slope_b * -2.303
# 切片からA, Bを求める
A = 10 ** intercept_p / (1 - np.exp(-alpha * T))
B = 10 ** intercept_q / (1 - np.exp(-beta * T))
 
print('A: {}, alpha: {}'.format(A, alpha))
print('B: {}, beta: {}'.format(B, beta))
 
plt.figure(figsize=(11, 6))
plt.subplots_adjust(wspace=0.35, hspace=0.35)
# plotのためx軸の値を作成
x = np.arange(0, 25, 0.01)
 
# 左側グラフ(片対数プロット)
plt.subplot(1, 2, 1)
# プロットはlogスケールで表示するので変換前の値にしておく
alpha_line = np.power(10, intercept_p + slope_a * (x - T))      # α相の直線
beta_line = np.power(10, intercept_q + slope_b * (x[500:] - T)) # β相の直線[500:]
beta_ex = np.power(10, intercept_q + slope_b * (x[:500] - T))   # β相の外挿部分[:499]
 
# 各直線のプロット
plt.plot(x, alpha_line, 'red', label='A='+str(round(A, 1))+', α='+str(round(alpha, 3)))
plt.plot(x[500:], beta_line, 'blue', label='B='+str(round(B, 1))+', β='+str(round(beta, 3)))
plt.plot(x[:500], beta_ex, 'blue', linestyle='--')
# 実測点 - β相の外挿線のプロット
plt.plot(t[:4], c_diff, '.', color='lime',
         label='実測値-β相の外挿線', alpha=0.6, markersize=8)
plt.yscale('log', basey=10)
plt.ylim(1, 200)
 
# 右側グラフ(ノーマルプロット)
plt.subplot(1, 2, 2)
time = np.arange(1, 25, 0.01)
c_form = A * (1 - np.exp(-alpha * T)) * np.exp(-alpha * (time - T)) \
        + B * (1 - np.exp(-beta * T)) * np.exp(-beta * (time - T))
plt.plot(time, c_form, 'magenta', label='$A(e^{-α(t-T)}-e^{-αt}) + B(e^{-β(t-T)}-e^{-βt})$')
plt.ylim(0, 60)
 
# 2つのグラフで共通する設定は以下で行う
axs = plt.gcf().get_axes()
for ax in axs:
    # current axsを設定
    plt.sca(ax)
    # 実測データをプロット
    plt.plot(t, c, '.', color='green', label='実測値', alpha=0.6, markersize=8)
    # 軸ラベルを表示
    plt.ylabel('血中濃度[μg/mL]')
    plt.xlabel('時間[hr]')
    # 横軸の範囲を指定する
    plt.xlim(0, 25)
    # グリッドの表示
    plt.grid(which='both', linestyle='dashed')
    # ラベルに応じた凡例を表示
    plt.legend()
plt.show()
 
 
# 上で得られた値を初期値として2コンパートメントモデルの点滴静注時の数式をフィッティングする.
# scipyのoptimize.leastsqを用いて非線形回帰を行い, A, alpha, B, betaを求める
init_param = [A, alpha, B, beta]
print('init_param :', init_param)
 
 
# パラメータをフィッティングしたい関数を定義する
def func(param, t, c, T=1.0):
    A = param[0]
    alpha = param[1]
    B = param[2]
    beta = param[3]
    return A * (np.exp(-alpha * (t-T)) - np.exp(-alpha * t)) \
        + B * (np.exp(-beta * (t-T)) - np.exp(-beta * t)) - c
 
 
result_param = optimize.leastsq(func, init_param, args=(t, c))
 
A = result_param[0][0]
alpha = result_param[0][1]
B = result_param[0][2]
beta = result_param[0][3]
 
k21 = (A * alpha * beta + B * alpha * beta) / (A * alpha + B * beta)
ke = (alpha * beta) / k21
k12 = alpha + beta - k21 - ke
Vd1 = x0 / T / (A * alpha + B * beta)
print('AUC(μg・hr/mL): ', (A + B) * T)
print('t_half(hr)(β相): ', np.log(2) / beta)
print('ke(hr^-1): ', ke)
print('k12(hr^-1): ', k12)
print('k21(hr^-1): ', k21)
print('CL(mL/min):', ke * Vd1 * 1000 / 60)
print('Vd1(L): ', Vd1)
print('Vss(L): ', Vd1 * (1 + k12 / k21))
 
 
# 2-コンパートメント点滴静注モデル
def calc_conc(time, A, alpha, B, beta, T=1.0):
    c = []
    for t in time:
        if t <= T:
            # 点滴開始～終了時
            c.append(A * (1 - np.exp(-alpha * t)) + B * (1 - np.exp(-beta * t)))
        else:
            # 点滴終了後
            c.append(A * (np.exp(-alpha * (t - T)) - np.exp(-alpha * t)) +
                    B * (np.exp(-beta * (t - T)) - np.exp(-beta * t)))
    return c
 
 
time = np.arange(0, 25, 0.01)
plt.plot(time, calc_conc(time, A, alpha, B, beta), color='red')
plt.plot(t, c, 'b.', label='実測値', alpha=0.6, markersize=8)
plt.ylabel('血中濃度[μg/mL]')
plt.xlabel('時間[hr]')
plt.ylim(0, 60)
plt.xlim(0, 25)
plt.grid(which='both', linestyle='dashed')
plt.legend()
plt.title('2-コンパートメント点滴静注モデル')
plt.show()

*1:インタビューフォームを参考にしていますが、グラフから私が読み取った値なので大体です。

*2:この点滴終了後の式はt>Tだったので、t=1.0のときの点は使うべきではないのかもしれませんが…t=0のときのcとして今回は使って計算しました。

*3:定積分するとそれぞれ複雑な数式が出てきますが、和をとるときれいになります

*4:インタビューフォームの値は今回のようなやり方で求めているのではありません。