半減期の長い薬物の場合は定常状態への到達が遅れます。このような薬物の場合、開始時期に投与量や回数を増やすことで目標とする血中濃度への到達を早める投与設計を行うことがあります。
今回はこれまで使ってきた2-コンパートメント点滴静注モデルのプログラムを不均等の間隔・投与量でも対応できるように変更して、テイコプラニンを負荷投与したときの血中濃度推移のグラフを描いてみようと思います。
プログラムを不均等(間隔・投与量)に対応させる
ベースは今まで使ってきたBloodConcTwoComp2クラスです。これまでは投与量・投与間隔とも何回目の投与でも同じでしたが、投与量が変わると計算式のパラメータA、Bの値が変化します。これを求めるメソッドを作り、投与量が変わるタイミングに合わせて適宜呼び出すようにします。
# 現在の投与量からA, Bを計算する def calc_param(self, idx): index = idx ko = self.x0[index] / self.T self.A = (ko * (self.alpha - self.k21)) / (self.Vc * self.alpha * (self.alpha - self.beta)) self.B = (ko * (self.k21 - self.beta)) / (self.Vc * self.beta * (self.alpha - self.beta))
現在の投与間隔を示すインデックスを受け取り、パラメータAとBを求めます。
ちなみに、このメソッドを__init__()で呼ぶことでもってself.Aとself.Bの初期化をしようと思っていたら、コードのチェック機能でエラーがかかりました。少し冗長な気もしますが、__init__()にself.A = self.B = Noneを書くことで対応しました。
次はコンストラクタです。
class BloodConcTwoComp3: STEP = 0.01 # x0: 投与量(mg)のタプル, CCr(mL/min), Wt(kg), # T: 点滴時間(hr), intervals: 投与間隔(hr)のタプル def __init__(self, x0, CCr, Wt, T, intervals): self.k21 = 0.0485 self.Vc = 10.4 k12 = 0.380 CL = 0.00498 * CCr + 0.00426 * Wt ke = CL / self.Vc s = self.k21 + k12 + ke p = self.k21 * ke self.alpha = (s + math.sqrt(s ** 2 - 4 * p)) / 2 self.beta = s - self.alpha self.A = self.B = None self.x0 = x0 self.T = T self.intervals = intervals self.idx = 0 # 現在の投与間隔のインデックス self.n = 1 # 何回目の投与かを表す self.calc_param(self.idx) self.ex_c = np.zeros(int(intervals[0] / self.STEP)) # 延長分濃度. 0で初期化 self.section_c = None # 1投与区間の血中濃度を格納. Cminを表示するのに使う
今まではコンストラクタの引数にA、B、alpha、betaを渡していましたが、CCr(クレアチニンクリアランス)とWt(体重)を渡してクラスの初期化時にこれらの値を計算します。
この点以外は、基本的に今までのクラスと同じです。注意点としては、x0(投与量)とintervals(投与間隔)は同じ長さのタプルとして渡す、くらいでしょうか(下に説明を書いています)。
なお、薬物動態パラメータは血清アルブミン値を考慮しないものとして、上記のものを使用します。
一番下にself.section_cという変数がありますが、後でTDMソフトの値と比較するため新たに作ったメソッドで使用するだけで、血中濃度の描画には関係ありません。
calc_section_conc()の中で1投与間隔分の血中濃度を受け取っておき、以下のメソッドでその中の最低値を返します。
# 投与毎の最低血中濃度 def get_cmin(self): return min(self.section_c)
他の変更点としては、上でも書きましたが、血中濃度の計算するメソッド(calc_during_div()とcalc_after_div())の直前にcalc_param()を呼ぶことくらいです。ページの最後にコードを載せてありますので、そちらを参照してください。
負荷投与(ローディング)
ではこれでコードを実行してみます。基本的なところの確認ですが、テイコプラニンは半減期が長く、定常状態に達するまでに長い時間が必要となります。そのため、初期に1回の投与量や1日投与回数を増やす負荷投与が必要となるのでした。この負荷投与を行うことにより、早くに目標の血中濃度に到達させることが可能となります。
負荷投与を行う場合と行わない場合のグラフを描いて、確認してみます。
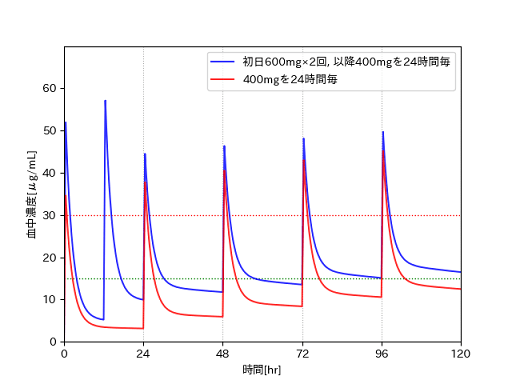
負荷投与を行っている青いグラフの方が、より早く治療濃度域に到達していることがわかります。
TDMソフトとの比較
作成したプログラムの血中濃度推移をテイコプラニンのTDM解析支援ソフトウェアiOS版TOWA-TDMと比較してみました。
このソフトでは「初期投与設計」から患者情報、投与計画を入力すると血中濃度推移が表示されます。このとき、各投与間隔毎にCmin(μg/mL)の値も出てくるので、この数値を自前のコードのものと比べて見てみます。
患者情報は適当ですが、男性、50歳、50kg、血清クレアチニンは1mg/dLとして、CCrは62.50mL/min、血清アルブミン値は考慮しない、を選びました。
投与量(mg)と投与間隔(hr)はプリセットの『ガイドライン4』を選んでみました。
次のような投与方法です(カッコ内が投与間隔)。
600(-), 600(12), 600(12), 600(12), 600(12), 400(24), 400(24)
これを点滴時間0.5hrで投与したとき各投与回におけるCmin(μg/mL)のソフトの表示は次のようになりました。
| 投与回数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Cmin(μg/mL) | 0 | 5.2 | 9.9 | 14.4 | 18.6 | 20.9 | 21.6 |
自前のコードで試す場合は、投与量と投与間隔のタプルは次のように設定します。
# x0とintervalsのタプルの長さは同じにする x0 = tuple([600] * 5 + [400] * 2) # 投与量(mg) intervals = tuple([12] * 4 + [24] * 3) # 投与間隔(hr)
1回目の投与間隔がソフトでは0となっていますが、私のコードでは0を入れませんので上のような表現の仕方になります。
実行結果は次のようになりました。
Cmin: 0.0 Cmin: 5.222655346539856 Cmin: 9.943765917476636 Cmin: 14.380742175884453 Cmin: 18.55128214657191 Cmin: 20.933439995710366 Cmin: 21.641678634359472
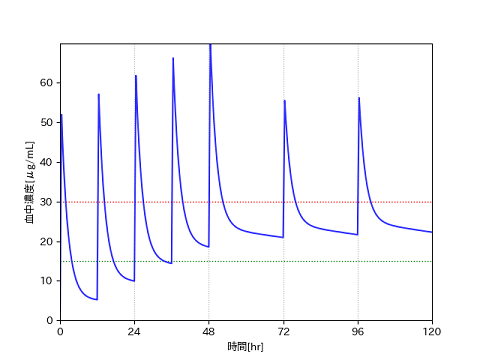
プリセットでは投与量や間隔にあまり変化がないので、実際にはなさそうな投与方法ですが、プログラムを確かめるということで次のような投与も試してみました。
600(-), 600(12), 400(24), 800(24), 800(12), 400(24), 400(12)
このときのソフトの表示は
| 投与回数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Cmin(μg/mL) | 0 | 5.2 | 9.2 | 11.2 | 17.5 | 21.5 | 23.7 |
自前のコードの実行結果は
Cmin: 0.0 Cmin: 5.222655346539856 Cmin: 9.158086829344597 Cmin: 11.238051982227814 Cmin: 17.52633783000333 Cmin: 21.543104169328096 Cmin: 23.730387607619353
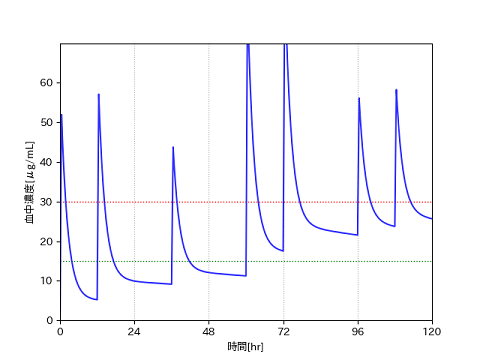
Cminの値を見る限りでは、不均等でもうまく描画できるようです。
最後に今回のコードを載せておきます。
import numpy as np import matplotlib.pyplot as plt import math # 2コンパートメントモデル繰り返し点滴静注の薬物血中濃度推移 # 不均等(間隔, 投与量)に対応 class BloodConcTwoComp3: STEP = 0.01 # x0: 投与量(mg)のタプル, CCr(mL/min), Wt(kg), # T: 点滴時間(hr), intervals: 投与間隔(hr)のタプル def __init__(self, x0, CCr, Wt, T, intervals): self.k21 = 0.0485 self.Vc = 10.4 k12 = 0.380 CL = 0.00498 * CCr + 0.00426 * Wt ke = CL / self.Vc s = self.k21 + k12 + ke p = self.k21 * ke self.alpha = (s + math.sqrt(s ** 2 - 4 * p)) / 2 self.beta = s - self.alpha self.A = self.B = None self.x0 = x0 self.T = T self.intervals = intervals self.idx = 0 # 現在の投与間隔のインデックス self.n = 1 # 何回目の投与かを表す self.calc_param(self.idx) self.ex_c = np.zeros(int(intervals[0] / self.STEP)) # 延長分濃度. 0で初期化 self.section_c = None # 1投与区間の血中濃度を格納. Cminを表示するのに使う # 現在の投与量からA, Bを計算する def calc_param(self, idx): index = idx ko = self.x0[index] / self.T self.A = (ko * (self.alpha - self.k21)) / (self.Vc * self.alpha * (self.alpha - self.beta)) self.B = (ko * (self.k21 - self.beta)) / (self.Vc * self.beta * (self.alpha - self.beta)) # 点滴開始~終了直前 def calc_during_div(self): td = np.linspace(0, self.T, num=int(self.T / self.STEP), endpoint=False) return self.A * (1 - np.exp(-self.alpha * td)) + self.B * (1 - np.exp(-self.beta * td)) # 点滴終了時~次回投与直前 def calc_after_div(self, begin, end): section = np.linspace(begin, end, num=int((end - begin) / self.STEP), endpoint=False) return self.A * (np.exp(-self.alpha * (section - self.T)) - np.exp(-self.alpha * section)) \ + self.B * (np.exp(-self.beta * (section - self.T)) - np.exp(-self.beta * section)) # 点滴開始から次回投与までの血中濃度を返す. # 今回投与分と前回投与時までの延長分(今回投与間隔分)の濃度の合計を足し合わせて返す. def calc_section_conc(self): self.calc_param(self.idx) c1 = self.calc_during_div() c2 = self.calc_after_div(self.T, self.intervals[self.idx]) c = np.concatenate([c1, c2], axis=0) # c1とc2を最初の軸(0次元目)で連結 sum_c = c + self.calc_extended_conc(self.n, self.ex_c) # 単回投与+延長分 self.section_c = sum_c # ここで1投与区間の濃度をもらっておき, get_cminで使用 # 次回投与時のために以下の変数を更新 self.n += 1 self.idx = (self.idx + 1) % len(self.intervals) self.ex_c = np.zeros(int(self.intervals[self.idx] / self.STEP)) # この初期化は必要 return sum_c.tolist() # 1回目~前回までの全ての投与回の延長(残存)分の血中濃度の合計を返す. # n: 投与回数, ex_c: 延長分の濃度の合計, begin: 求めるべき延長分濃度の計算開始位置 def calc_extended_conc(self, n, ex_c, begin=0): if n == 1: return ex_c else: prev_idx = (n - 2) % len(self.intervals) # 1つ前の投与間隔のインデックス prev_interval = self.intervals[prev_idx] begin += prev_interval end = begin + self.intervals[self.idx] self.calc_param(prev_idx) ex_c += self.calc_after_div(begin, end) return self.calc_extended_conc(n-1, ex_c, begin) # 投与毎の最低血中濃度 def get_cmin(self): return min(self.section_c) if __name__ == '__main__': # 注意点: x0とintervalsのタプルの長さは同じにする CCr = 62.5 # クレアチニンクリアランス(mL/min) Wt = 50 # 体重(kg) T = 0.5 # 点滴時間(hr) # こちらを試す場合はインスタンス生成, 辞書部分も適宜変更すること # iOS版TOWA-TDMの「ガイドライン4」と同じ # graphlabel_1 = 'TOWA-TDMガイドライン4' # x0_1 = tuple([600] * 5 + [400] * 2) # 投与量(mg) # intervals_1 = tuple([12] * 4 + [24] * 3) # 投与間隔(hr) # cycle1 = 1 # 実際にはなさそうな投与方法 # graphlabel_2 = '実際にはなさそうな投与方法' # x0_2 = tuple([600] * 2 + [400] + [800] * 2 + [400] * 2) # intervals_2 = tuple([12] + [24] * 2 + [12, 24, 12, 12]) # cycle2 = 1 # ローディングあり(blue) graphlabel_1 = '初日600mg×2回, 以降400mgを24時間毎' x0_1 = tuple([600] * 2 + [400] * 4) intervals_1 = tuple([12] * 2 + [24] * 4) cycle1 = 1 # intervalsを何サイクル繰り返すか bc1 = BloodConcTwoComp3(x0_1, CCr, Wt, T, intervals_1) # ローディングなし(red) graphlabel_2 = '400mgを24時間毎' x0_2 = (400, ) intervals_2 = (24, ) cycle2 = 5 bc2 = BloodConcTwoComp3(x0_2, CCr, Wt, T, intervals_2) conc1, conc2 = [], [] # 辞書に登録. key: グラフの色 bc = {'blue': (bc1, conc1, cycle1, graphlabel_1), 'red': (bc2, conc2, cycle2, graphlabel_2)} for color, value in bc.items(): _bc, conc, cycle, g_label = value print(g_label) for _ in range(len(_bc.intervals) * cycle): conc.extend(_bc.calc_section_conc()) print('Cmin:',_bc.get_cmin()) period = sum(_bc.intervals) * cycle # グラフの描画区間 time = np.linspace(0, period, num=int(period / BloodConcTwoComp3.STEP), endpoint=False) plt.plot(time, conc, color=color, alpha=0.8, label=g_label) plt.hlines(y=30, xmin=0, xmax=period, color='red', linestyles='dotted', linewidth=1) plt.hlines(y=15, xmin=0, xmax=period, color='green', linestyles='dotted', linewidth=1) plt.ylabel('血中濃度[μg/mL]') plt.xlabel('時間[hr]') plt.xticks(np.arange(0, time[-1] + 24, 24)) plt.yticks(np.arange(0, 70, 10)) plt.xlim(0, period) plt.ylim(0, 70) plt.legend() plt.grid(linestyle='dotted', axis='x') plt.show()