PK/PDパラメータのCmax/MIC, AUC/MICを求める

今回も引き続きPK/PDパラメータについてです。前回は
www.yakupro.info

でTime above MICを求めるコードを書きましたが、今回はCmax/MICとAUC/MICを求めるメソッドを実装しようと思います。コードはあまり複雑な部分はなく、簡単に書くことができました。

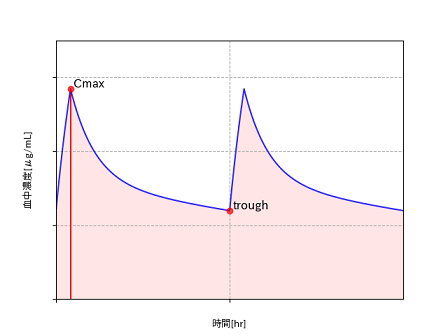
Cmax/MIC

最高血中濃度をMICで割った値で、濃度依存性抗菌薬のアミノグリコシド系やキノロン系などで有効性の指標とされます。このような抗菌薬では１日量を分割して投与するよりも１回で投与する方がより有効な投与方法として推奨されます。

    def get_cmax_mic(self, mic):
        return max(self.last_interval) / mic

1-コンパートメント点滴静注モデルのときは計算式を使ってCmaxを得るようにしましたが、前回使ったself.last_interval（定常状態の投与間隔の血中濃度）から最大値を組み込み関数のmax()を使って取得しています。ちなみに、トラフ値の場合はリストから最小値を取得するmin()を使って以下のように書くことができます。

    def get_trough(self):
        return min(self.last_interval)

AUC/MIC

AUCをMICで割った値。この値が重要な指標となる薬剤にはキノロン系やアミノグリコシド系、バンコマイシンなどがあるようです。

    # AUC24/MIC
    def get_auc_mic(self, mic):
        n = 24 / self.intervals[0]  # 1日の投与回数
        return (self.A + self.B) * self.T * n / mic

24時間のAUCを求めるため1日の投与回数をかけています。また、AUCについてですが「バンコマイシンの血中濃度データに2-コンパートメントモデルを当てはめる」でみたように薬物動態が線形の場合、2-コンパートメント点滴静注モデルでは投与間隔のAUCは以下の式で求められました。

ちょっと脇道にそれますが、scipyの数値積分の値を上の数式の値と比べてみました。

    # AUCの解析的な値
    def analytic_auc(self):
        return (self.A + self.B) * self.T
 
    # scipyの数値積分によるAUC
    def numerical_auc(self):
        # 点滴開始~点滴終了までの区間で定積分
        auc1 = integrate.quad(
            lambda t: self.A * (1 - np.exp(-self.alpha * t)) + self.B * (1 - np.exp(-self.beta * t)),
            0, self.T)

        # 点滴終了~次回時までの区間で定積分
        auc2 = integrate.quad(
            lambda t: self.A * (np.exp(-self.alpha * (t - self.T)) - np.exp(-self.alpha * t)) \
                      + self.B * (np.exp(-self.beta * (t - self.T)) - np.exp(-self.beta * t)),
            self.T, np.inf)

        return auc1[0] + auc2[0]

バンコマイシンでCCr50mL/min、体重50kg, 投与量500mg、点滴時間1hr、投与間隔12時間でこれらのメソッドの結果は以下のようになりました。

numerical_auc:  258.9331952356303
analytic_auc:   258.93319523562957

数値積分による値には誤差が含まれていますが、この場合誤差についてはほぼ無視できる程度のようです。しかしモンテカルロシミュレーションなどで何千～何万回と繰り返し計算するような場合には、解析的な値を求める方法と比較すると処理時間の差が馬鹿にできないほど大きくなってきます。

TDM解析ソフトとの比較

定常状態における最大血中濃度、最小血中濃度、をソフトの値と比較してみました。
比較に使用したソフトはバンコマイシン「MEEK」TDM解析ソフトVer.1.0です。「母集団平均値による初期投与設計」でCCr50mL/min、体重50kg、投与量500mg、点滴時間1hr, 投与間隔12時間での数値は

最大血中濃度	最小血中濃度
33.8	17.2	518.1

でした。自前のコードでは、CmaxとAUC24はメソッドの引数をmic=1としてget_cmax_mic()とget_auc_mic()を呼んで表示（Cmax/1, AUC24/1ということ）、定常状態は半減期の７倍とした値です。

最大血中濃度:  33.643879236793225
最小血中濃度:  16.998985013928937
AUC24:  517.8663904712591

全部少し低いですね・・・。 いろいろとパラメータを変えてやってみたところ、どうやら数値の丸め処理や定常状態までを半減期の何倍とするか、あたりが差の原因かな。私のコードの正確性を保証するものではありませんのでご注意を。

最後に今回のコードです。

import numpy as np
import math
 
# PK/PDパラメータのCmax/MIC, AUC/MICを求める
 
class BloodConcTwoComp2:
    STEP = 0.01 # 経過時間の刻み幅
    MAGNI = 7  # 半減期の何倍で定常状態とするか
 
    def __init__(self, A, alpha, B, beta, T, intervals):
        self.A = A
        self.alpha = alpha
        self.B = B
        self.beta = beta
        self.T = T
        self.intervals = intervals
        self.idx = 0  # 現在の投与間隔のインデックス
        self.n = 1    # 何回目の投与かを表す
        self.ex_c = [0 for _ in range(int(intervals[0] / self.STEP))]  # 延長分濃度. 0で初期化
        t_half = np.log(2) / beta
        # 投与間隔の倍数のうち、半減期のMAGNI倍以上の最小値を定常状態到達時間とする
        self.css_t = (t_half * self.MAGNI // intervals[0] + 1) * intervals[0]
        # 定常状態までの繰り返し投与回数. 最低3回
        cycle_to_css = 3 if self.css_t // intervals[0] < 3 else int(self.css_t / intervals[0])
        c = []
        for _ in range(cycle_to_css):
            c.extend(self.calc_section_conc())
        self.last_interval = c[-int(self.intervals[0] / self.STEP):]
        # グラフ描画もするつもりならここでself.nを1に戻すこと
 
    # 点滴開始～終了直前
    def calc_during_div(self):
        td = np.linspace(0, self.T, num=int(self.T / self.STEP), endpoint=False)
        return self.A * (1 - np.exp(-self.alpha * td)) + self.B * (1 - np.exp(-self.beta * td))
 
    # 点滴終了時～次回投与直前
    def calc_after_div(self, begin, end):
        section = np.linspace(begin, end, num=int((end - begin) / self.STEP), endpoint=False)
        return self.A * (np.exp(-self.alpha * (section - self.T)) - np.exp(-self.alpha * section)) \
               + self.B * (np.exp(-self.beta * (section - self.T)) - np.exp(-self.beta * section))
 
    # 点滴開始から次回投与までの血中濃度を返す.
    # 今回投与分と前回投与時までの延長分(今回投与間隔分)の濃度の合計を足し合わせて返す.
    def calc_section_conc(self):
        c1 = self.calc_during_div()
        c2 = self.calc_after_div(self.T, self.intervals[self.idx])
        c = np.concatenate([c1, c2], axis=0)  # c1とc2を最初の軸(0次元目)で連結
        sum_c = c + self.calc_extended_conc(self.n, self.ex_c)  # 単回投与＋延長分
        # 次回投与時のために以下の変数を更新
        self.n += 1
        self.idx = (self.idx + 1) % len(self.intervals)
        return sum_c.tolist()
 
    # 1回目~前回までの全ての投与回の延長(残存)分の血中濃度の合計を返す.
    # n: 投与回数, ex_c: 延長分の濃度の合計, begin: 求めるべき延長分濃度の計算開始位置
    def calc_extended_conc(self, n, ex_c, begin=0):
        if n == 1:
            return ex_c
        else:
            prev_idx = (n - 2) % len(self.intervals)  # 1つ前の投与間隔のインデックス
            prev_interval = self.intervals[prev_idx]
            begin += prev_interval
            end = begin + self.intervals[self.idx]
            ex_c += self.calc_after_div(begin, end)
            return self.calc_extended_conc(n - 1, ex_c, begin)
 
    # %T>MIC
    def get_time_above_mic(self, mic):
        above_mic = len([c for c in self.last_interval if c > mic])
        tau = len(self.last_interval)
        return above_mic / tau * 100
 
    # Cmax/MIC
    def get_cmax_mic(self, mic):
        return max(self.last_interval) / mic
 
    # AUC24/MIC
    def get_auc_mic(self, mic):
        n = 24 / self.intervals[0]      # 1日の投与回数
        return (self.A + self.B) * self.T * n / mic
 
    # トラフ値
    def get_trough(self):
        return min(self.last_interval)
 

if __name__ == '__main__':
 
    CCr = 50            # クレアチニンクリアランス(mL/min)
    Wt = 50             # 体重(kg)
    x0 = 500            # 投与量(mg)
    T = 1               # 点滴時間(hr)
    intervals = (12, )  # 投与間隔
 
    # バンコマイシンTDMソフト「MEEK」の薬物動態パラメータを使用
    if CCr >= 85:
        CL = 3.83
    else:
        CL = 0.537 * CCr * 60 / 1000 + 0.32  # L/h
 
    Vc = 2.32 * 0.206 * Wt  # 中央コンパートメントの分布容積(L)
    Vt = 60.5578            # 抹消コンパートメントの分布容積(L)
    Q = 8.81                # コンパートメント間における血流速度(L/h)
    k12 = Q / Vc            # 中央→抹消コンパートメントへの消失速度定数(hr^-1)
    k21 = Q / Vt            # 抹消→中央コンパートメントへの消失速度定数(hr^-1)
    ke = CL / Vc
 
    X = k12 + k21 + ke      # alpha + beta
    Y = k21 * ke            # alpha * beta
    alpha = (X + math.sqrt(X ** 2 - 4 * Y)) / 2
    beta = X - alpha
    A = (x0 / T * (k21 - alpha)) / (Vc * alpha * (beta - alpha))
    B = (x0 / T * (k21 - beta)) / (Vc * (alpha - beta) * beta)
 
    bc = BloodConcTwoComp2(A, alpha, B, beta, T, intervals)
 
    print('最大血中濃度: ', bc.get_cmax_mic(1))
    print('最小血中濃度: ', bc.get_trough())
    print('AUC24: ', bc.get_auc_mic(1))
 

参考

薬局　抗菌化学療法のマネジメント 2009 Vol.60