前回は乱数でPKパラメータを生成するところまでやりました。今回は、これらのパラメータをもとに用法・用量を設定して血中濃度推移を計算していきます。内容的には前回の続きとなります。
www.yakupro.info
%T>MIC値の確認
これから血中濃度推移を計算していこうというところですが、その前に、まず自前のコードで%T>MICの値が正しく出るかを確認しておきます。
参考文献「薬理学的観点からみた PK-PD 理論とブレイクポイント」にはCCrが(高い・低い)、体重が(大きい・小さい)の組み合わせを想定し、メロペネム0.5gを0.5時間で点滴静注した後の血中濃度推移における、MICを4μg/mLとした場合の%T>MICの例が載っています。これを自前のコードでやってみると以下のようになりました。
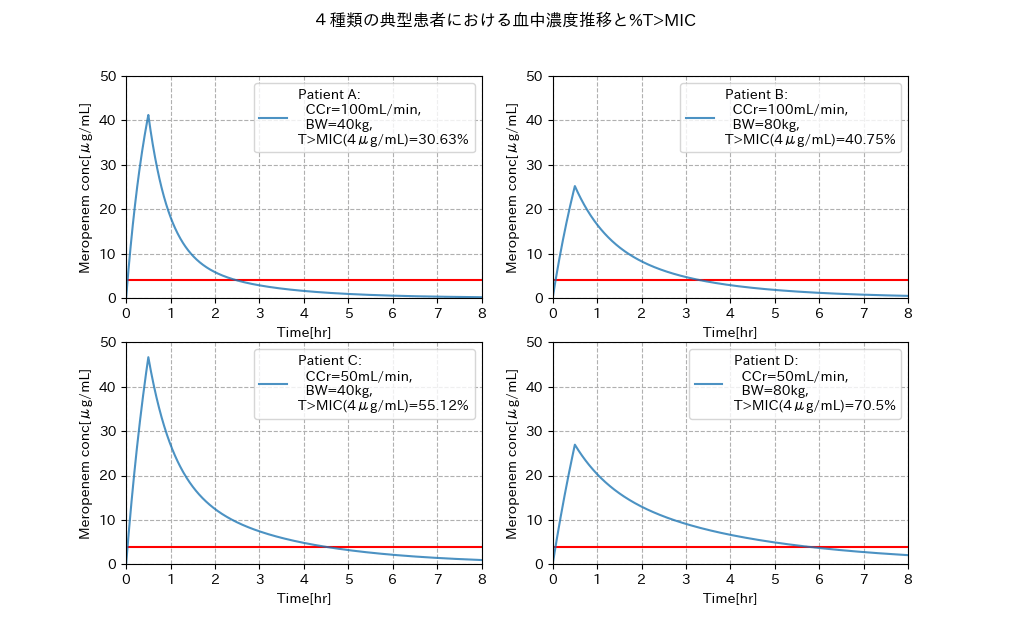
コードは以前の記事「PK/PDパラメータのTime above MICを求める」で作成したクラスを使いますが、ここでは参考文献に合わせてコードを少し変更しています。クラスのget_time_above_mic()メソッドでは定常状態における%T>MICを取得していましたが、参考文献では血中濃度が0からの推移になっていたので、コードの方も初回投与時における%T>MICを求めるよう変更しました(コードは長くなるので最後に載せておきます)。
参考文献のPatient A~Dの%T>MICを見てみると順に30.7%、40.8%、55.3%、70.5%となっています。自前のコードの結果では、まったく一緒にはなりませんでしたが、まずまずの数字と言えそうです。
用法・用量を設定し血中濃度推移を求める
前回記事でいうところの手順2、3に当たる部分です。
PKパラメータを10,000例発生させたので、10,000例のメロペネムの血中濃度推移が得られます。各投与方法毎に1回の用量と投与間隔は異なるので、ループを回して、その中で10,000例の血中濃度推移を求めることにしました。
from collections import OrderedDict T = 0.5 # 点滴時間 # 血中濃度推移に対して試すMIC(μg/mL)のリスト mic_list = np.array([0.063, 0.125, 0.25, 0.5, 1, 2, 4, 8, 16, 32, 64, 128]) # 順序が保持される辞書を使用 recipe = OrderedDict() # key: 投与方法 # value: (投与量(mg), 1日の投与回数, グラフ表示マーカー(o:丸, ^:三角, s:四角)) recipe = {'0.25g twice': (250, 2, 'o'), '0.25g 3 times': (250, 3, 'o'), '0.5g twice': (500, 2, '^'), '0.5g 3 times': (500, 3, '^'), '1g twice': (1000, 2, 's'), '1g 3 times(daily)': (1000, 3, 's')} # 発生させたパラメータから血中濃度計算に必要なalpha, betaを求める ke = X_cl / X_vc # CL / Vc k12 = X_q / X_vc # Q / Vc k21 = X_q / X_vp # Q / Vp s = k12 + k21 + ke # alpha + beta p = k21 * ke # alpha * beta alpha = (s + np.sqrt(s ** 2 - 4 * p)) / 2 beta = s - alpha for dosage, value in recipe.items(): x0 = value[0] # 投与量 k0 = x0 / T # 点滴速度(mg/hr) = 投与量 / 点滴時間 intervals = (int(24 / value[1]), ) # 投与間隔(hr) = 24 / 投与回数 # MICリストの要素数×サンプルサイズの行列. ここに%T>MICを格納していく data_matrix = np.zeros((len(mic_list), sample_size)) # 発生させたパラメータから血中濃度計算に必要なA, Bを求める A = (k0 * (alpha - k21)) / (X_vc * alpha * (alpha - beta)) B = (k0 * (k21 - beta)) / (X_vc * (alpha - beta) * beta) for i in range(sample_size): bc = BloodConcTwoComp2(A[i], alpha[i], B[i], beta[i], T, intervals)
コードは前回書いたものの続きになります。投与方法(投与量、回数)を辞書型recipeとして作成し、各投与方法毎にループで回していくというやり方です。
ノーマルの辞書だとリストと違って要素の順序は不定*1ですが、OrderedDictを使用することで項目が追加された順序を保つことができます。ループ内で投与量、投与回数を取り出し、クラスに渡すパラメータA、Bを求めます。αとβについては投与量や投与回数は関係ないので、ループの外で先に計算しておきます。
ここで確認しておきますが、発生させたPKパラメータ同士の算術計算(X_cl / X_vc等)は、numpy配列の各要素ごとで演算が行われます。例を見てみます。
>>> import numpy as np >>> x = np.array([[1, 2], [3, 4]]) >>> y = np.array([[2, 3], [4, 5]]) >>> x # 2行2列 array([[1, 2], [3, 4]]) >>> y array([[2, 3], [4, 5]]) >>> x * y # 各要素ごとの積になる array([[ 2, 6], [12, 20]])
また、numpy配列と単一の数値(スカラ値)の計算の場合は、ブロードキャストという機能により、あたかもnumpy配列同士の演算のように各要素に対してスカラ値が適用されます。
>>> x * 2 array([[2, 4], [6, 8]])
あと変数data_matrixについてですが、コメントに書いてある通り、ここに%T>MICを格納していきます。行数をMICリストの要素数、列数をサンプルサイズとして初期化しています。イメージとしては下の表のようなかんじです。

血中濃度推移に対しMICを設定し%T>MICを求める
for si in range(sample_size): bc = BloodConcTwoComp2(A[si], alpha[si], B[si], beta[si], T, intervals) for mi, mic in enumerate(mic_list): data_matrix[mi, si] = bc.get_time_above_mic(mic) # MIC=1の%T>MICの度数分布 plt.hist(data_matrix[4, :], bins=100, color='blue', alpha=0.4, ec='black', label=dosage +'\nMIC=1μg/mL') # 40%T>MICを境界にして塗りつぶし plt.axvspan(0, 40, color='green', alpha=0.2) plt.axvspan(40, 100, color='red', alpha=0.2) plt.ylabel('Frequency') plt.xlabel('%T>MIC') plt.xlim(0, 100) plt.legend() plt.show()
上のコードと一部重複しています。生成したインスタンスに対してMICを順次試していくようにするため、もう一度ループを回しています。
mi, siはdata_matrixの行、列を制御するインデックスとして使用しています。そして10,000例のMICリスト分の%T>MICをdata_matrixに格納した後、各用法におけるMIC=1μg/mL(1という数字に意味はありません)のときの%T>MICの度数分布をグラフにしています。
%T>MICの度数分布
CCr=100、Wt=80、0.25gを1日2回投与のときの分布を見てみると、以下のようになりました。
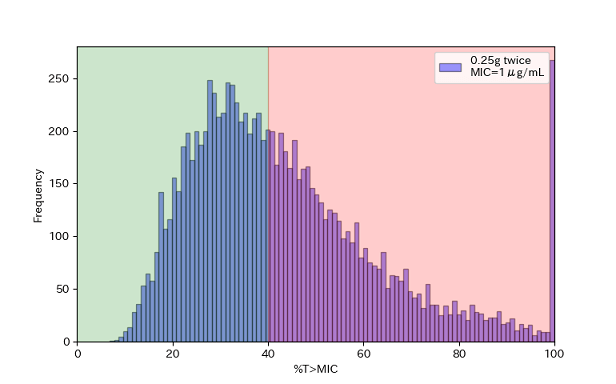
よく見てもらうとわかるのですが、右端の100%の度数が一番多くなっています(少ない場合もあるけど投与方法の違いによってはもっと極端に多くなる)。
どうやら原因はパラメータA、α、B、βのうちBの値が大きな値を取る場合にこのような%T>MICとなるようですが、このようになるものなのか、はっきりわかりません。最終的な結果だけをみてると、ほぼ参考文献と同じものが得られていると思うのですが。
あと、もう一つ、飛ばしたところがあります。参考文献では『薬物血中濃度(遊離型濃度)推移』とあります。この点について、いろいろ調べたところ、こちらの文献モンテカルロシミュレーションに対応したMicrosoft ® Office Excel による抗菌薬の PK / PDシミュレーションソフトの開発では『f:血漿蛋白非結合型分率×臓器移行率』として投与量に乗じています。
このブログ記事の場合は血中濃度(遊離型濃度)ベースなので臓器移行率は考えなくて良いかもしれませんが、蛋白結合率を考慮せずにコードを書いています。ちなみに、メロペネムの蛋白結合率は約2.5%とかなり小さいようです。(1 - 0.025)を投与量に乗じてもいいのかもしれませんが、今回はなしでやっています。
ところで、出来たコードを見るとfor文の3重ループになっており、もう少し見やすいコードに改善したいところです。「PK/PDパラメータのTime above MICを求める」でも書いたまま出来ていませんでしたが、この辺は後でまとめてコードの改善に取り組もうと思います。
長くなってきたので、次回に続きます。
今回は前半4つのグラフのコードと、モンテカルロシミュレーションの続きのコード2つを載せておきます。
import numpy as np import matplotlib.pyplot as plt import math # 4種類の典型患者の初回投与時における%T>MICを求める class BloodConcTwoComp2: STEP = 0.01 # 経過時間の刻み幅 def __init__(self, A, alpha, B, beta, T, intervals): self.A = A self.alpha = alpha self.B = B self.beta = beta self.T = T self.intervals = intervals self.idx = 0 # 現在の投与間隔のインデックス self.n = 1 # 何回目の投与かを表す self.ex_c = [0 for _ in range(int(intervals[0] / self.STEP))] # 延長分濃度. 0で初期化 # 1回目の投与で%T>MICを求めるよう変更 self.last_interval = self.calc_section_conc() self.n = 1 # 点滴開始~終了直前 def calc_during_div(self): td = np.linspace(0, self.T, num=int(self.T / self.STEP), endpoint=False) return self.A * (1 - np.exp(-self.alpha * td)) + self.B * (1 - np.exp(-self.beta * td)) # 点滴終了時~次回投与直前 def calc_after_div(self, begin, end): section = np.linspace(begin, end, num=int((end - begin) / self.STEP), endpoint=False) return self.A * (np.exp(-self.alpha * (section - self.T)) - np.exp(-self.alpha * section)) \ + self.B * (np.exp(-self.beta * (section - self.T)) - np.exp(-self.beta * section)) # 点滴開始から次回投与までの血中濃度を返す. # 今回投与分と前回投与時までの延長分(今回投与間隔分)の濃度の合計を足し合わせて返す. def calc_section_conc(self): c1 = self.calc_during_div() c2 = self.calc_after_div(self.T, self.intervals[self.idx]) c = np.concatenate([c1, c2], axis=0) # c1とc2を最初の軸(0次元目)で連結 sum_c = c + self.calc_extended_conc(self.n, self.ex_c) # 単回投与+延長分 # 次回投与時のために以下の変数を更新 self.n += 1 self.idx = (self.idx + 1) % len(self.intervals) return sum_c.tolist() # 1回目~前回までの全ての投与回の延長(残存)分の血中濃度の合計を返す. # n: 投与回数, ex_c: 延長分の濃度の合計, begin: 求めるべき延長分濃度の計算開始位置 def calc_extended_conc(self, n, ex_c, begin=0): if n == 1: return ex_c else: prev_idx = (n - 2) % len(self.intervals) # 1つ前の投与間隔のインデックス prev_interval = self.intervals[prev_idx] begin += prev_interval end = begin + self.intervals[self.idx] ex_c += self.calc_after_div(begin, end) return self.calc_extended_conc(n - 1, ex_c, begin) # %T>MICを計算する def get_time_above_mic(self, mic): above_mic = len([c for c in self.last_interval if c > mic]) tau = len(self.last_interval) return above_mic / tau * 100 if __name__ == '__main__': x0 = 500 # 投与量(mg) T = 0.5 # 点滴時間(hr) intervals = (8, ) # 投与間隔 cycle = 1 # intervalsを何サイクル繰り返すか mic = 4 # 4種類の典型患者のCCrとWt typical_pt = {'Patient A': (100, 40), 'Patient B': (100, 80), 'Patient C': (50, 40), 'Patient D': (50, 80)} plt.figure() plt.suptitle('4種類の典型患者における血中濃度推移と%T>MIC') for i, (pt, param) in enumerate(typical_pt.items()): CCr = param[0] # クレアチニンクリアランス(mL/min) Wt = param[1] # 体重(kg) CL = 0.0905 * CCr + 2.03 # L/h Vc = Wt * 0.199 # 中央コンパートメントの分布容積(L) Vt = 4.55 # 抹消コンパートメントの分布容積(L) Q = 4.02 # コンパートメント間における血流速度(L/h) k12 = Q / Vc # 中央→抹消コンパートメントへの消失速度定数(hr^-1) k21 = Q / Vt # 抹消→中央コンパートメントへの消失速度定数(hr^-1) ke = CL / Vc p = k12 + k21 + ke # alpha + beta s = k21 * ke # alpha * beta alpha = (p + math.sqrt(p ** 2 - 4 * s)) / 2 beta = p - alpha A = (x0 / T * (alpha - k21)) / (Vc * alpha * (alpha - beta)) B = (x0 / T * (k21 - beta)) / (Vc * beta * (alpha - beta)) # パラメータを渡してインスタンスを生成 bc = BloodConcTwoComp2(A, alpha, B, beta, T, intervals) # グラフラベルの作成 graphlabel = pt + ':\n CCr=' + str(CCr) + 'mL/min,\n BW=' + str(Wt) + \ 'kg,\nT>MIC(4μg/mL)=' + str(round(bc.get_time_above_mic(mic), 2)) + '%' print(graphlabel) conc = [] conc.extend(bc.calc_section_conc()) plt.subplot(2, 2, i + 1) period = sum(bc.intervals) * cycle # グラフの描画区間 time = np.linspace(0, period, num=int(period / BloodConcTwoComp2.STEP), endpoint=False) plt.plot(time, conc, alpha=0.8, label=graphlabel) plt.hlines(y=mic, xmin=0, xmax=intervals[0], color='red') plt.ylabel('Meropenem conc[μg/mL]') plt.xlabel('Time[hr]') plt.xticks(np.arange(0, intervals[0]+0.1, 1)) plt.yticks(np.arange(0, 50+1, 10)) plt.xlim(0, intervals[0]) plt.ylim(0, 50) plt.legend() plt.grid(linestyle='dashed') plt.show()
次がモンテカルロシミュレーション(続き)のコードです。
import numpy as np import matplotlib.pyplot as plt from collections import OrderedDict # 抗菌薬でモンテカルロシミュレーション2 class BloodConcTwoComp2: STEP = 0.01 # 経過時間の刻み幅 MAGNI = 7 # 半減期の何倍で定常状態とするか def __init__(self, A, alpha, B, beta, T, intervals): self.A = A self.alpha = alpha self.B = B self.beta = beta self.T = T self.intervals = intervals self.idx = 0 # 現在の投与間隔のインデックス self.n = 1 # 何回目の投与かを表す self.ex_c = [0 for _ in range(int(intervals[0] / self.STEP))] # 延長分濃度. 0で初期化 t_half = np.log(2) / beta # 投与間隔の倍数のうち、半減期のMAGNI倍以上の最小値を定常状態到達時間とする self.css_t = (t_half * self.MAGNI // intervals[0] + 1) * intervals[0] # 定常状態までの繰り返し投与回数. 最低3回 cycle_to_css = 3 if self.css_t // intervals[0] < 3 else int(self.css_t / intervals[0]) c = [] for _ in range(cycle_to_css): c.extend(self.calc_section_conc()) self.last_interval = c[-int(self.intervals[0] / self.STEP):] # 点滴開始~終了直前 def calc_during_div(self): td = np.linspace(0, self.T, num=int(self.T / self.STEP), endpoint=False) return self.A * (1 - np.exp(-self.alpha * td)) + self.B * (1 - np.exp(-self.beta * td)) # 点滴終了時~次回投与直前 def calc_after_div(self, begin, end): section = np.linspace(begin, end, num=int((end - begin) / self.STEP), endpoint=False) return self.A * (np.exp(-self.alpha * (section - self.T)) - np.exp(-self.alpha * section)) \ + self.B * (np.exp(-self.beta * (section - self.T)) - np.exp(-self.beta * section)) # 点滴開始から次回投与までの血中濃度を返す. # 今回投与分と前回投与時までの延長分(今回投与間隔分)の濃度の合計を足し合わせて返す. def calc_section_conc(self): c1 = self.calc_during_div() c2 = self.calc_after_div(self.T, self.intervals[self.idx]) c = np.concatenate([c1, c2], axis=0) # c1とc2を最初の軸(0次元目)で連結 sum_c = c + self.calc_extended_conc(self.n, self.ex_c) # 単回投与+延長分 # 次回投与時のために以下の変数を更新 self.n += 1 self.idx = (self.idx + 1) % len(self.intervals) return sum_c.tolist() # 1回目~前回までの全ての投与回の延長(残存)分の血中濃度の合計を返す. # n: 投与回数, ex_c: 延長分の濃度の合計, begin: 求めるべき延長分濃度の計算開始位置 def calc_extended_conc(self, n, ex_c, begin=0): if n == 1: return ex_c else: prev_idx = (n - 2) % len(self.intervals) # 1つ前の投与間隔のインデックス prev_interval = self.intervals[prev_idx] begin += prev_interval end = begin + self.intervals[self.idx] ex_c += self.calc_after_div(begin, end) return self.calc_extended_conc(n - 1, ex_c, begin) # %T>MICを計算する def get_time_above_mic(self, mic): above_mic = len([c for c in self.last_interval if c > mic]) tau = len(self.last_interval) return above_mic / tau * 100 if __name__ == '__main__': sample_size = 10000 CCr = 100 # クレアチニンクリアランス(mL/min) Wt = 80 # 体重(kg) CL = 0.0905 * CCr + 2.03 Vc = 0.199 * Wt T = 0.5 # 点滴時間 # seedを設定し発生する乱数を固定する. np.random.seed(1234) # 引数で指定した形状(4×sample_size)の標準正規乱数を生成 X = np.random.randn(4, sample_size) # 各PKパラメータの分布は対数正規分布を仮定する X_cl = CL * np.exp(X[0, :] * 0.411) # CL(L/h) X_vc = Vc * np.exp(X[1, :] * 0.398) # Vc(L) X_q = 4.02 * np.exp(X[2, :] * 0.328) # Q(L/h) X_vp = 4.55 * np.exp(X[3, :] * 0.299) # Vp(L) # 血中濃度推移に対して試すMIC(μg/mL)のリスト mic_list = np.array([0.063, 0.125, 0.25, 0.5, 1, 2, 4, 8, 16, 32, 64, 128]) # 順序が保持される辞書を使用 recipe = OrderedDict() # key: 投与方法 # value: (投与量(mg), 1日の投与回数, グラフ表示マーカー(o:丸, ^:三角, s:四角)) recipe = {'0.25g twice': (250, 2, 'o'), '0.25g 3 times': (250, 3, 'o'), '0.5g twice': (500, 2, '^'), '0.5g 3 times': (500, 3, '^'), '1g twice': (1000, 2, 's'), '1g 3 times(daily)': (1000, 3, 's')} # 発生させたパラメータから血中濃度計算に必要なalpha, betaを求める ke = X_cl / X_vc # CL / Vc k12 = X_q / X_vc # Q / Vc k21 = X_q / X_vp # Q / Vp s = k12 + k21 + ke # alpha + beta p = k21 * ke # alpha * beta alpha = (s + np.sqrt(s ** 2 - 4 * p)) / 2 beta = s - alpha for dosage, value in recipe.items(): x0 = value[0] # 投与量 k0 = x0 / T # 点滴速度(mg/hr) = 投与量 / 点滴時間 intervals = (int(24 / value[1]), ) # 投与間隔(hr) = 24 / 投与回数 # MICリストの要素数×サンプルサイズの行列. ここに%T>MICを格納していく data_matrix = np.zeros((len(mic_list), sample_size)) # 発生させたパラメータから血中濃度計算に必要なA, Bを求める A = (k0 * (alpha - k21)) / (X_vc * alpha * (alpha - beta)) B = (k0 * (k21 - beta)) / (X_vc * beta * (alpha - beta)) for si in range(sample_size): bc = BloodConcTwoComp2(A[si], alpha[si], B[si], beta[si], T, intervals) for mi, mic in enumerate(mic_list): data_matrix[mi, si] = bc.get_time_above_mic(mic) # MIC=1の%T>MICの度数分布 print(dosage) plt.hist(data_matrix[4, :], bins=100, color='blue', alpha=0.4, ec='black', label=dosage +'\nMIC=1μg/mL') # 40%T>MICを境界にして塗りつぶし plt.axvspan(0, 40, color='green', alpha=0.2) plt.axvspan(40, 100, color='red', alpha=0.2) plt.ylabel('Frequency') plt.xlabel('%T>MIC') plt.xlim(0, 100) plt.legend() plt.show()
参考
1. 薬理学的観点からみた PK-PD 理論とブレイクポイント
2.モンテカルロシミュレーションに対応したMicrosoft ® Office Excel による抗菌薬の PK / PDシミュレーションソフトの開発
*1:Python3.7からは辞書の順序が保証されているそうです。私のバージョンは3.6なのでこうしています。