PK/PDパラメータのTime above MICを求める

抗菌薬のPK/PDパラメータ

PK/PDとは薬物動態学（用法・用量と抗菌薬の濃度推移の関係）と薬力学（抗菌薬の濃度と有効性・副作用の関係）を組み合わせることにより、抗菌薬の有効性や安全性を評価する考え方のことです。
その重要なパラメータにtime above MIC, Cmax/MIC, AUC/MICがありますが、抗菌薬によってどのパラメータが効果と相関するかは異なります。また、これらの指標を使うことによってより有効で安全な投与設計をすることが可能となります。今回はこれらのパラメータのうちtime above MICを求めるコードを書こうと思います。

Time above MICとは

抗菌薬の血中濃度がMICを超えている時間のことで、定常状態における投与間隔に対するこの時間の割合（％）を％T＞MICと表記します。
βラクタム系などの時間依存性抗菌薬の効果がこの％T＞MICと相関し、一般にこのような抗菌薬は一回の投与量を増やすよりも、%T>MICが増加するよう分割投与が行われます。また、その目標値は一般に40％以上が一つの目安とされており、この目標値を達成できるように抗菌薬の投与量や投与方法を選択する必要があります。

%T>MICを求める

単純に投与回数を増やせば%T>MICを高めることはできそうですが、投与量をどれくらいで何時間の投与間隔で投与すれば目標値を達成できるかを推定できればより有用性が高まるとのこと。
ここでは１-コンパートメントモデル、２-コンパートメントモデルでも同じように求めることができるやり方を今まで作ってきたクラスにメソッドとして実装します。
これまでのクラスではSTEP(経過時間の刻み幅)=0.01として、血中濃度は「投与間隔 / STEP」の長さのリストで得ていました。定常状態に達した後の投与間隔の血中濃度のリストから、ＭＩＣを超える要素の個数をカウントすることで%T>MICを求めます。これを前回作った２-コンパートメントモデルのクラスBloodConcTwoComp2に実装しました。

    def get_time_above_mic(self, mic):
        above_mic = len([c for c in self.last_interval if c > mic])
        tau = len(self.last_interval)
        return above_mic / tau * 100

self.last_intervalは定常状態後の投与間隔の血中濃度のリストです。これを内包表記でMICを超える要素だけを取り出し、len()でその要素数を取得しています。具体的な例で示すと、以下のような感じです。

>>> mic = 2
>>> last_interval = [1, 2, 3, 4, 4, 3, 2, 1]    # 定常状態後の血中濃度
>>> above_mic = [c for c in last_interval if c > mic]
>>> above_mic
[3, 4, 4, 3]
>>> len(above_mic)
4

ここで、self.last_intervalという新たなインスタンス変数が出てきていますが、これはコンストラクタ内で取得しておきます。

    t_half = np.log(2) / beta
    # 投与間隔の倍数のうち、半減期の5倍以上の最小値を定常状態到達時間とする
    self.css_t = (t_half * 5 // intervals[0] + 1) * intervals[0]
    # 定常状態までの繰り返し投与回数. 最低3回
    cycle_to_css = 3 if self.css_t // intervals[0] < 3 else self.css_t // intervals[0]
    c = []
    for _ in range(cycle_to_css):
        c.extend(self.calc_section_conc())
    self.last_interval = c[-int(self.intervals[0] / self.STEP):]
    self.n = 1    # カウンタが進んでしまうので1に戻しておく. グラフ描画もするなら必要

少しごちゃごちゃしてきました。やりたいことは、定常状態後の投与間隔分の血中濃度self.last_intervalを取得することです。
定常状態までの繰り返し投与回数分self.calc_section_conc()を呼び血中濃度のリストを生成、最後に投与間隔分スライスしています。ここで、半減期(β相)によっては定常状態までの繰り返し回数が1回になることがあったのですが、それだと後々都合が悪い（後で作るトラフ値を取得するメソッドでトラフが０になってしまう場合がある）ので、最低３回は繰り返すようにしています。
仮にMICを5として、このメソッドのabove_micの部分を赤いラインで描画してみると次のようになりました。(描画部分のコードはここには書いていません)

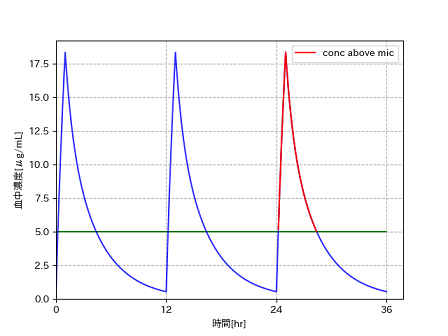
拡大してみると、僅かに誤差（MICより上の時間ぴったりではない）が見て取れます。STEPをもっと小さくすると、よりこの誤差を小さく出来ますが処理が重くなるのでこのままでいきます。
インスタンス生成後、このメソッドの引数にMICを渡して次のように呼び出します。

# %T>MICが知りたいだけなら, インスタンス生成後にこのようにメソッドを呼ぶだけで良い.   
print('%T>MIC(5): ', bc.get_time_above_mic(5))

ちなみに、情報が古いかもしれませんが、手元にあった本（「薬局　抗菌化学療法のマネジメント 2009 Vol.60」）には以下のような%T>MICを簡単に計算する方法が紹介されていました（一部抜粋）。

単純に１-コンパートメントモデルとして、投与0時間時点での予想血中濃度()からMICの濃度に落ちるまでの時間を求める、というやり方です。しかしこれでは点滴開始からCmaxまでの時間は反映されません。もっと正確な求め方はないかな、と思ってネットで検索していたら、より正確な計算方法がこちら（モンテカルロシミュレーションに対応したMicrosoft ® Office Excel による抗菌薬の PK / PDシミュレーションソフトの開発）に載っていました。ここでは紹介しませんが、実際にやってみたら、１-コンパートメントモデルではより正確な%T>MICが計算できました。

コードにはまだ改善すべき点がありますが、後でまとめて取り組みます。
とりあえず今回はこれまで。

参考

薬局　抗菌化学療法のマネジメント 2009 Vol.60

import numpy as np
import matplotlib.pyplot as plt
import math
 
# PK/PDパラメータのTime above MICを求める
 
class BloodConcTwoComp2:
    STEP = 0.01   # 経過時間の刻み幅
    MAGNI = 5     # 半減期の何倍で定常状態とするか
 
    def __init__(self, A, alpha, B, beta, T, intervals):
        self.A = A
        self.alpha = alpha
        self.B = B
        self.beta = beta
        self.T = T
        self.intervals = intervals
        self.idx = 0    # 現在の投与間隔のインデックス
        self.n = 1      # 何回目の投与かを表す
        self.ex_c = [0 for _ in range(int(intervals[0] / self.STEP))]  # 延長分濃度. 0で初期化
        t_half = np.log(2) / beta
        # 投与間隔の倍数のうち、半減期のMAGNI倍以上の最小値を定常状態到達時間とする
        self.css_t = (t_half * self.MAGNI // intervals[0] + 1) * intervals[0]
        # 定常状態までの繰り返し投与回数. 最低3回
        cycle_to_css = 3 if self.css_t // intervals[0] < 3 else int(self.css_t / intervals[0])
        c = []
        for _ in range(cycle_to_css):
            c.extend(self.calc_section_conc())
        self.last_interval = c[-int(self.intervals[0] / self.STEP):]
        self.n = 1    # カウンタが進んでしまうので1に戻しておく. グラフ描画もするなら必要
 
    # 点滴開始～終了直前
    def calc_during_div(self):
        td = np.linspace(0, self.T, num=int(self.T / self.STEP), endpoint=False)
        return self.A * (1 - np.exp(-self.alpha * td)) + self.B * (1 - np.exp(-self.beta * td))
 
    # 点滴終了時～次回投与直前
    def calc_after_div(self, begin, end):
        section = np.linspace(begin, end, num=int((end - begin) / self.STEP), endpoint=False)
        return self.A * (np.exp(-self.alpha * (section - self.T)) - np.exp(-self.alpha * section)) \
               + self.B * (np.exp(-self.beta * (section - self.T)) - np.exp(-self.beta * section))
 
    # 点滴開始から次回投与までの血中濃度を返す.
    # 今回投与分と前回投与時までの延長分(今回投与間隔分)の濃度の合計を足し合わせて返す.
    def calc_section_conc(self):
        c1 = self.calc_during_div()
        c2 = self.calc_after_div(self.T, self.intervals[self.idx])
        c = np.concatenate([c1, c2], axis=0)  # c1とc2を最初の軸(0次元目)で連結
        sum_c = c + self.calc_extended_conc(self.n, self.ex_c)  # 単回投与＋延長分
        # 次回投与時のために以下の変数を更新
        self.n += 1
        self.idx = (self.idx + 1) % len(self.intervals)
        return sum_c.tolist()
 
    # 1回目~前回までの全ての投与回の延長(残存)分の血中濃度の合計を返す.
    # n: 投与回数, ex_c: 延長分の濃度の合計, begin: 求めるべき延長分濃度の計算開始位置
    def calc_extended_conc(self, n, ex_c, begin=0):
        if n == 1:
            return ex_c
        else:
            prev_idx = (n - 2) % len(self.intervals)  # 1つ前の投与間隔のインデックス
            prev_interval = self.intervals[prev_idx]
            begin += prev_interval
            end = begin + self.intervals[self.idx]
            ex_c += self.calc_after_div(begin, end)
            return self.calc_extended_conc(n - 1, ex_c, begin)
 
    # %T>MIC
    def get_time_above_mic(self, mic):
        above_mic = len([c for c in self.last_interval if c > mic])
        tau = len(self.last_interval)
        return above_mic / tau * 100
 
 
if __name__ == '__main__':
    CCr = 40            # クレアチニンクリアランス(mL/min)
    Wt = 50             # 体重(kg)
    x0 = 500            # 投与量(mg)
    T = 0.5             # 点滴時間(hr)
    intervals = (12, )  # 投与間隔
    cycle = 3           # intervalsを何サイクル繰り返すか
    mic = 5             # MICを設定
    graphlabel = 'MEPM500mg×12時間毎'
 
    # MEPMの母集団パラメータを使用して計算
    CL = 0.091 * CCr + 2.03    # L/h
    Vc = Wt * 0.199            # 中央コンパートメントの分布容積(L)
    Vt = 4.55                  # 抹消コンパートメントの分布容積(L)
    Q = 4.02                   # コンパートメント間における血流速度(L/h)
    k12 = Q / Vc               # 中央→抹消コンパートメントへの消失速度定数(hr^-1)
    k21 = Q / Vt               # 抹消→中央コンパートメントへの消失速度定数(hr^-1)
    ke = CL / Vc
 
    X = k12 + k21 + ke         # alpha + beta
    Y = k21 * ke               # alpha * beta
    alpha = (X + math.sqrt(X ** 2 - 4 * Y)) / 2
    beta = X - alpha
 
    A = (x0 / T * (k21 - alpha)) / (Vc * alpha * (beta - alpha))
    B = (x0 / T * (k21 - beta)) / (Vc * (alpha - beta) * beta)
 
    # パラメータを渡してインスタンスを生成
    bc = BloodConcTwoComp2(A, alpha, B, beta, T, intervals)
    # %T>MICが知りたいだけなら, インスタンス生成後にこのメソッドを呼ぶだけで良い.
    print('%T>MIC(' + str(mic) + '): ', bc.get_time_above_mic(mic))
 
    conc1 = []
    bc = {'blue': (bc, conc1, cycle, graphlabel)}
 
    for color, value in bc.items():
        _bc, conc, cycle, g_label = value
        for _ in range(len(_bc.intervals) * cycle):
            conc.extend(_bc.calc_section_conc())
        period = sum(_bc.intervals) * cycle  # グラフの描画区間
        time = np.linspace(0, period, num=int(period / BloodConcTwoComp2.STEP), endpoint=False)
        plt.plot(time, conc, color=color, alpha=0.8, label=g_label)
        plt.hlines(mic, xmin=0, xmax=period, color='red', linestyles='dashed')
 
    plt.ylabel('血中濃度[μg/mL]')
    plt.xlabel('時間[hr]')
    plt.xticks(np.arange(0, time[-1] + 12, 12))
    plt.xlim(0, )
    plt.ylim(0, )
    plt.grid(linestyle='dashed')
    plt.legend()
    plt.show()