前回はある程度時間が経ってからの血中濃度を近似的に計算する方法を使いプログラムを書きましたが、誤差が大きく使えそうもありませんでした。今回は別の方法で繰り返し投与の実装を考えます。

血中濃度の足し合わせによる方法
今回実装する方法は、次のようなやり方です。
図中には描かれていませんが、連続投与2回目の濃度は1回目投与時の血中濃度残存分(赤の点線)+2回目に単独投与された分の血中濃度となります。では、3回目では2回目の残存分+3回目の投与分となるのですが、この2回目の残存分というのは1回目と2回目の単独投与時の残存分(3つ目の山の緑と赤の点線部分)のことです。同様に、4回目投与時の山は、1、2、3回目投与時の残存分(水色と緑と赤の点線部分)+4回目投与分の合計ということになります。
要するに、単回投与時の濃度をそれまでの分すべて足し合わせていく方法です。
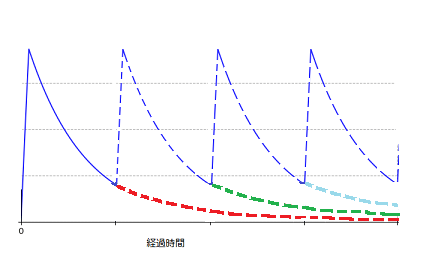
この考え方で繰り返し投与を実装したいと思います。
再帰関数
今回は再帰関数を用いて書いてみることにしました。再帰関数とはその関数の中で自分自身を呼び出す構造を持つ関数のことです。ちょっと、簡単な例で見てみます。
# 階乗n!を計算 def factorial(n): if n == 0: return 1 else: return n * factorial(n - 1)
階乗(1から n までの全ての整数をかけ算した値)を求める関数です。
処理を追っていくと、nが0になるまで自身を引数n-1で呼び出し続けます。そしてnが0になったとき、再帰呼び出しがなくなり1を返します。そして、呼び出し元に戻る→呼び出し元に戻る・・・となり、最終的に最初に呼ばれたところに帰ってきます。
この階乗計算などはfor文を使って書いてもそれほど複雑ではなく、再帰関数で書く必要性があまりないかもしれませんが、アルゴリズムによっては簡潔でわかりやすいプログラムが書けることがあります。
今回のケースでは、1回目~(今回投与ー1)回目までの残存分の血中濃度の合計を求める部分を再帰関数で実装します。
再帰関数で実装する
いろいろな考え方があるとは思いますが、私は以下のように考えていきました。
まず、返すべき値は1回目~前回投与までの全ての投与回の延長(残存)分の血中濃度の合計です。下図をみてください。たとえば、投与回数(n)が4回目のときの場合は1~3回目までの区間[begin-end]間の点線部分(赤、緑、水色)の合計となります。
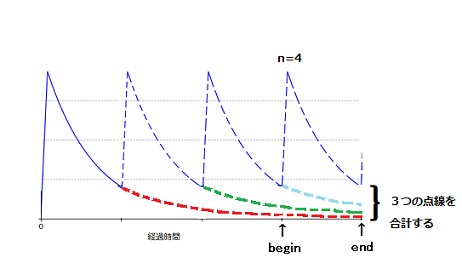
投与回数をnとしたので、これを関数の引数として考えてみます。
上の例で示した階乗の関数のように、再帰呼び出し時にn-1を渡し、前回、前々回・・・と遡って延長分の血中濃度を求めていくことにします。
そしてnが1ずつ小さくなっていき、n=1(1回目の投与)まで遡ったときが再帰呼び出しの終了条件となります。これをif~else節で書くと次のようになります。
# n: 投与回数 def 合計を返す再帰関数(n): if n == 1: return 投与1回目の延長分濃度 else: n回目のbegin~end間の血中濃度を求める処理 return 合計を返す再帰関数(n-1)
ここで、投与1回目の場合を考えてみます。1回目投与時は、合計すべき延長分の血中濃度はありません。なので、この関数を呼び出しても0を返さなくてはいけません。
うーん、どうしようか・・・、今までのこの手の私のプログラムでは延長分の濃度はコンストラクタ内で0で初期化していました。これをそのまま使おう、ということでこれも関数の引数とし、1回目投与時は初期化された延長分の血中濃度をそのまま返すようにしました。
ここまですると後はだいたい固まってくるのですが、引数として渡された空の(0で初期化された)延長分の濃度、これにelse節で求めた濃度を合算していくことにします。ここまでを言葉で書くと以下のようになります。
# n: 投与回数, ex_c: 延長分の濃度 def 合計を返す再帰関数(n, ex_c): if n == 1: return ex_c else: c = n回目のbegin~end間の血中濃度 ex_c += c return 合計を返す再帰関数(n-1, ex_c)
あとは変数beginとendを求める部分です。これもいろいろ悩んだのですが、再帰呼び出しが深くなるごとにbeginも更新されていくので、結局関数の引数としてbeginを渡すことにしました。上の例のn=4で投与間隔が12時間毎の場合、beginとendは次のようにならなくてはいけません。
begin: 12, end: 24 # 水色 begin: 24, end: 36 # 緑色 begin: 36, end: 48 # 赤色
完成したコードはこのようになりました。
# 1回目~前回までの全ての投与回の延長(残存)分の血中濃度の合計を返す. # n: 投与回数, ex_c: 延長分の濃度の合計, begin: 求めるべき延長分濃度の計算開始位置 def calc_extended_conc(self, n, ex_c, begin=0): if n == 1: return ex_c else: prev_idx = (n - 2) % len(self.intervals) # 1つ前の投与間隔のインデックス prev_interval = self.intervals[prev_idx] begin += prev_interval end = begin + self.intervals[self.idx] ex_c += self.calc_after_div(begin, end) return self.calc_extended_conc(n-1, ex_c, begin)
これまでと違う点について説明します。
点滴終了時~次回投与直前の濃度を計算するメソッド(calc_after_div)は再帰関数の中でも使うため、引数にbegin, endを受けるようにして関数内で区間を作ってから計算するよう変えています。また、これまでは濃度の合算はリスト内包表記を使っていましたが、np.array配列のまま+=で求めるように変更しました。
呼び出し側のコードは次のようになります。
# 点滴開始から次回投与までの血中濃度を返す. # 今回投与分と前回投与時までの延長分(今回投与間隔分)の濃度の合計を足し合わせて返す. def calc_section_conc(self): c1 = self.calc_during_div() c2 = self.calc_after_div(self.T, self.intervals[self.idx]) c = np.concatenate([c1, c2], axis=0) # c1とc2を最初の軸(0次元目)で連結 sum_c = c + self.calc_extended_conc(self.n, self.ex_c) # 次回投与時のために以下の変数を更新 self.n += 1 self.idx = (self.idx + 1) % len(self.intervals) return sum_c.tolist()
グラフ描画部分のコードを変えたくなかったので、最後のreturnのところでsum_cは結局リストに変換しています。
近似式バージョンのグラフとの比較
ではこれでグラフを描いてみます。
前回作成のプログラムとの違いがはっきりするように、投与間隔は6時間と短く、他の条件は同じ(CCr=50, Wt=50, バンコマイシンTDMソフト「MEEK」の薬物動態パラメータを使用)で比べてみました。
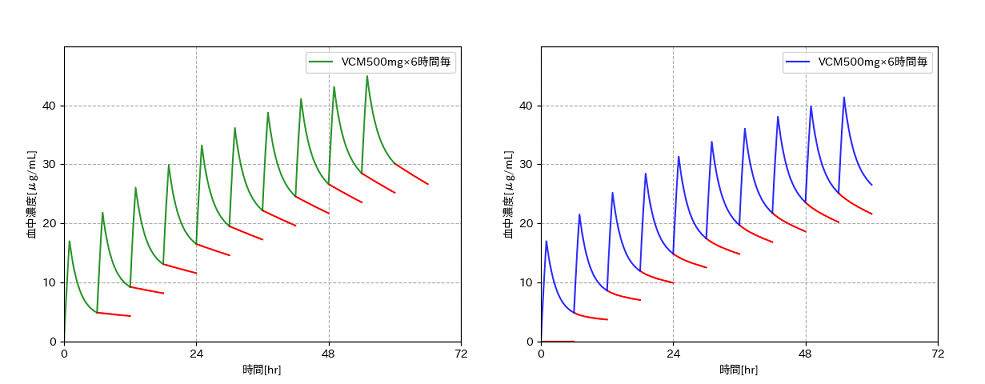
左が投与終了5時間後以降を1-コンパートメントで近似したグラフ、右が今回作成した再帰によって残存分を求めたグラフです。
赤いラインはどちらも前回投与の残存(延長)分の濃度を示しますが、今回のプログラムの方がより自然な形になっているのがわかります。10回目の投与直前で左のグラフとの差が3μg/mL以上ありました。
では、12時間毎の投与の場合はどうでしょうか。1-コンパートメントでの近似は投与終了10時間後以降としています。
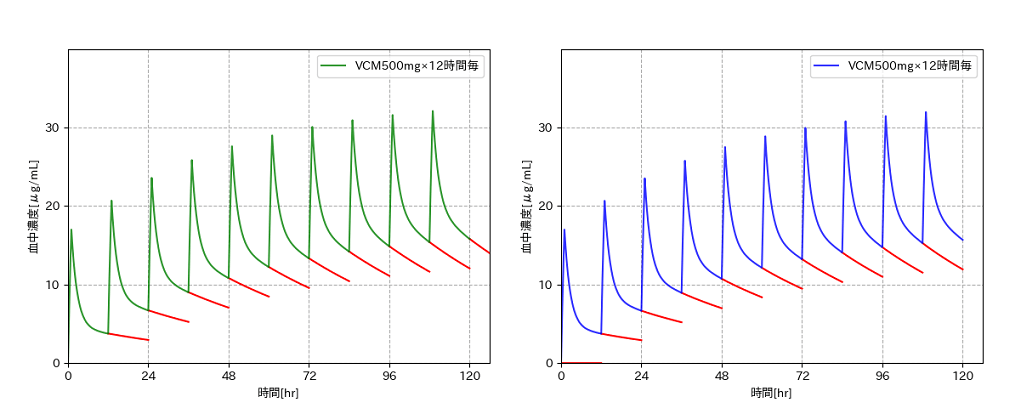
このケースでは、10回目の投与直前でも0.14μg/mL程度とほぼ違いはありませんでした。実際、赤いラインも左右で大きな違いはないように見えます。しかし、A、B、α、βのパラメータによっては、たとえ投与間隔が長くてもこのケースより誤差が大きくなるような場合もあるかと考えられます。
今回は再帰関数で繰り返し投与をプログラムしてみました。引数をもっとシンプルにしたい、とか、再帰が深くなっていけば濃度はほぼゼロになるのだから適当なところで再帰を打ち切ってもいいんじゃないか、とか改善の余地はまだありそうですが、再帰のプログラムとしては取りあえずこれで完成とします。
再帰関数でなくたって良い
最後にもう1点、プログラミングの話です。このプログラムでは再帰関数を使っているので、繰り返し投与の回数cycleを大きな数*1に設定すると、(試していませんが)メモリのスタック領域がオーバーフローしてプログラムが停止する可能性があります。
再帰関数はややコードが直感的に書けるという部分もありますが、今回のような再帰の場合(末尾再帰というそうです)は、forループを使って次のように簡単に書き直すことができます。
def calc_extended_conc(self, n, ex_c, begin=0): for n in range(n, 1, -1): # range(start, stop, step) prev_idx = (n - 2) % len(intervals) # 1つ前の投与間隔のインデックス prev_interval = self.intervals[prev_idx] begin += prev_interval end = begin + self.intervals[self.idx] ex_c += self.calc_after_div(begin, end) else: return ex_c
さらにここからコードを改善してみます。
今回のプログラムのボトルネックは(おそらく)calc_after_div()です。できるだけこのメソッドの呼び出しを少なくするよう上のコードをさらに改善したものがこちらです。
# 注: コンストラクタにself.accum_c=Noneを書いておく def calc_extended_conc(self, n, ex_c, begin=0): if self.n >= 2: for n in range(n, 1, -1): # range(start, stop, step) prev_idx = (n - 2) % len(intervals) # 1つ前の投与間隔のインデックス prev_interval = self.intervals[prev_idx] begin += prev_interval end = begin + self.intervals[self.idx] else: self.accum_c = self.calc_after_div(begin, end) return self.accum_c else: self.accum_c = ex_c return ex_c
試しに、cycle=100で血中濃度生成ループの処理時間とcalc_after_div()メソッドの呼び出し回数を計測*2してみたところ、私の環境では次のようになりました。
- 上(改善前)のコード:処理時間(sec) 0.2922・・, 呼び出し回数 5050
- 下(改善後)のコード:処理時間(sec) 0.0179・・, 呼び出し回数 199
以上、コードの改善によって処理時間が変わってくるという話でした。
今回のコード全文です。
import numpy as np import matplotlib.pyplot as plt import math # 2コンパートメントモデル繰り返し点滴静注の薬物血中濃度推移 # 再帰関数バージョン class BloodConcTwoComp2: STEP = 0.01 def __init__(self, A, alpha, B, beta, T, intervals): self.A = A self.alpha = alpha self.B = B self.beta = beta self.T = T self.intervals = intervals self.idx = 0 # 現在の投与間隔のインデックス self.n = 1 # 何回目の投与かを表す self.ex_c = [0 for _ in range(int(intervals[0] / self.STEP))] # 延長分濃度. 0で初期化 # 点滴開始~終了直前 def calc_during_div(self): td = np.linspace(0, self.T, num=int(self.T / self.STEP), endpoint=False) return self.A * (1 - np.exp(-self.alpha * td)) + self.B * (1 - np.exp(-self.beta * td)) # 点滴終了時~次回投与直前 def calc_after_div(self, begin, end): section = np.linspace(begin, end, num=int((end - begin) / self.STEP), endpoint=False) return self.A * (np.exp(-self.alpha * (section - self.T)) - np.exp(-self.alpha * section)) \ + self.B * (np.exp(-self.beta * (section - self.T)) - np.exp(-self.beta * section)) # 点滴開始から次回投与までの血中濃度を返す. # 今回投与分と前回投与時までの延長分(今回投与間隔分)の濃度の合計を足し合わせて返す. def calc_section_conc(self): c1 = self.calc_during_div() c2 = self.calc_after_div(self.T, self.intervals[self.idx]) c = np.concatenate([c1, c2], axis=0) # c1とc2を最初の軸(0次元目)で連結 sum_c = c + self.calc_extended_conc(self.n, self.ex_c) # 単回投与+延長分 # 次回投与時のために以下の変数を更新 self.n += 1 self.idx = (self.idx + 1) % len(self.intervals) return sum_c.tolist() # 1回目~前回までの全ての投与回の延長(残存)分の血中濃度の合計を返す. # n: 投与回数, ex_c: 延長分の濃度の合計, begin: 求めるべき延長分濃度の計算開始位置 def calc_extended_conc(self, n, ex_c, begin=0): if n == 1: # 延長分の血中濃度をグラフに表示しない場合は以下2行をコメントアウト s = np.linspace(begin, begin + self.intervals[self.idx], num=int(self.intervals[self.idx] / self.STEP), endpoint=False) plt.plot(s, ex_c, 'r-') return ex_c else: prev_idx = (n - 2) % len(self.intervals) # 1つ前の投与間隔のインデックス prev_interval = self.intervals[prev_idx] begin += prev_interval end = begin + self.intervals[self.idx] ex_c += self.calc_after_div(begin, end) return self.calc_extended_conc(n-1, ex_c, begin) if __name__ == '__main__': CCr = 50 # クレアチニンクリアランス(mL/min) Wt = 50 # 体重(kg) x0 = 500 # 投与量(mg) T = 1 # 点滴時間(hr) intervals = (12,) # 投与間隔 cycle = 10 # intervalsを何サイクル繰り返すか graphlabel = 'VCM500mg×12時間毎' # バンコマイシンTDMソフト「MEEK」の薬物動態パラメータを使用 if CCr >= 85: CL = 3.83 else: CL = 0.537 * CCr * 60 / 1000 + 0.32 # L/h Vc = 2.32 * 0.206 * Wt # 中央コンパートメントの分布容積(L) Vt = 60.5578 # 抹消コンパートメントの分布容積(L) Q = 8.81 # コンパートメント間における血流速度(L/h) k12 = Q / Vc # 中央→抹消コンパートメントへの消失速度定数(hr^-1) k21 = Q / Vt # 抹消→中央コンパートメントへの消失速度定数(hr^-1) ke = CL / Vc X = k12 + k21 + ke # alpha + beta Y = k21 * ke # alpha * beta alpha = (X + math.sqrt(X ** 2 - 4 * Y)) / 2 beta = X - alpha A = (x0 / T * (k21 - alpha)) / (Vc * alpha * (beta - alpha)) B = (x0 / T * (k21 - beta)) / (Vc * (alpha - beta) * beta) print(A, B) print(alpha, beta) # パラメータを渡してインスタンスを生成 bc = BloodConcTwoComp2(A, alpha, B, beta, T, intervals) conc1 = [] bc = {'blue': (bc, conc1, cycle, graphlabel)} for color, value in bc.items(): _bc, conc, cycle, g_label = value for _ in range(len(_bc.intervals) * cycle): conc.extend(_bc.calc_section_conc()) period = sum(_bc.intervals) * cycle # グラフの描画区間 time = np.linspace(0, period, num=int(period / BloodConcTwoComp2.STEP), endpoint=False) plt.plot(time, conc, color=color, alpha=0.8, label=g_label) plt.ylabel('血中濃度[μg/mL]') plt.xlabel('時間[hr]') plt.xticks(np.arange(0, time[-1] + 24, 24)) plt.yticks(np.arange(0, 40, 10)) plt.xlim(0,) plt.ylim(0,) plt.legend() plt.grid(linestyle='dashed') plt.show()