引き続き1-コンパートメント点滴静注モデルです。今回は不均等の時間間隔投与(例えば、初回12時間、2回目12時間、3回目以降24時間や、投与回ごとに投与量が異なる場合の血中濃度推移を描画できるプログラムを作りたいと思います。
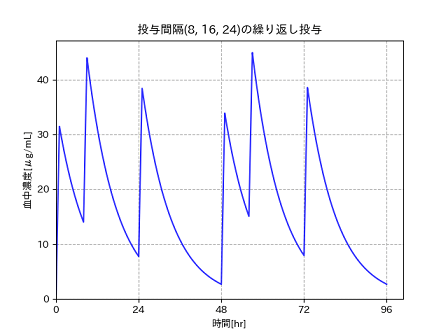
一般化された式を使わずに繰り返し投与を描く
今まではn回目投与時の血中濃度の計算式にn=1、2、3・・・と渡していき、それらを繋ぎ合わせていくことで描画していましたが、投与間隔が不均等の場合、この式はそのまま使うことはできません(不均等の場合でも一般化された公式があるようですが)。
そこで別の方法で繰り返し投与時の血中濃度を求める方法を考えます。
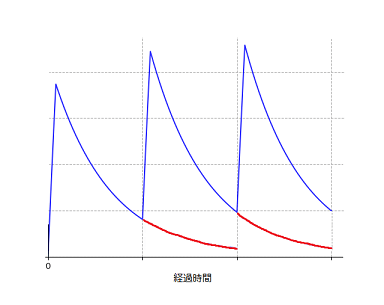
図のように、2回目以降の血中濃度は、1つ前の投与時の血中濃度残存分(図の赤いライン部分)+単回投与時の血中濃度ということになります。投与間隔が均等でなくても、1つ前の残存分がわかればいいわけです。これだと一般化された式を使わなくても不均等間隔での血中濃度を求めることができそうです。
点滴終了後の血中濃度
点滴終了後の血中濃度は、1-コンパートメントモデルなので点滴終了時をとすると、以降は一次速度で減少していきますから、
で求めることができます。
単回投与時の血中濃度の計算式については、こちらの記事を参考にしてみてください。
・1-コンパートメント点滴静注モデルの血中濃度推移 - 薬剤師のプログラミング学習日記
血中濃度残存分を計算するメソッド
上図赤いライン部分の濃度を計算するコードです。
def calc_extended_conc(self, intervals): begin = self.interval - self.T n_idx = (self.idx + 1) % len(intervals) # 次回投与間隔のインデックス next_interval = intervals[n_idx] end = begin + next_interval ex_t = np.linspace(begin, end, num=int((end - begin) / 0.01), endpoint=False) extended_c = self._cmax * np.exp(-self._k * ex_t) return extended_c
引数はintervalsとして投与間隔のタプルを取ります。例えば投与間隔が8、16、24時間を1サイクルとする繰り返し投与の場合、あらかじめ次のように初期化しておきます。
intervals = (8, 16, 24)
また、インデックスを指定することで各要素を取得することができます。
>>> intervals[0] 8 >>> intervals[1] 16 >>> intervals[2] 24
具体的な例でみてみます。T(点滴時間)=1で8、16、24時間の間隔で3回投与するとして、各投与間隔ごとにBloodConcインスタンスを生成します。その後、投与間隔8時間のインスタンスのcalc_extended_conc(上記のメソッド)を呼び出したときの状態を下の図のように考えます。
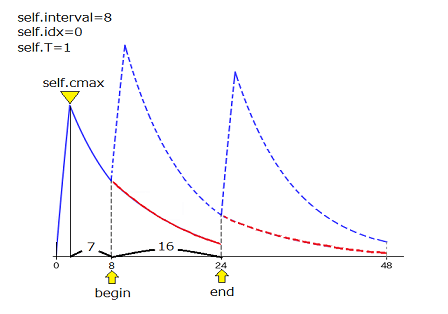
図中ではbegin、endはそれぞれ8と24を指していますが、実際にはself.cmaxからの経過時間である7と23が入ります。これらの数字を元に区間ex_t(次回投与間隔分の時間)を生成し、血中濃度extended_c(赤のライン部分)を求めています。このextended_cを次の投与(投与間隔16時間)のインスタンスに渡し、このインスタンスが単回投与の血中濃度と足し合わせることで目的とする血中濃度を得ることになります。
次回投与間隔のインデックスを取得する部分は次のように書いています。
n_idx = (self.idx + 1) % len(intervals) # 次回投与間隔のインデックス
このように書くことで自分が0番目(self.idx=0)ならn_idxは1、self.idx=1ならn_idxは2、self.idx=2ならn_idxは0となります。
では、次に赤のライン部分と単回投与の血中濃度を足し合わせるメソッドです。
def calc_section_conc(self, extended_c): c1 = self.__calc_during_div() c2 = self.__calc_after_div() c1.extend(c2) sum_c = [sc + ec for sc, ec in zip(c1, extended_c)] if self.interval == self.T: max_pos = int(self.T / 0.01) - 1 else: max_pos = int(self.T / 0.01) self.cmax = sum_c[max_pos] return sum_c
引数に先ほどのメソッドで計算した延長血中濃度(赤いライン部分)のリストを受け取っていますが、 c1.extend(c2)までは今までのクラスと同じです。
実際に足し合わせる処理は
[sc + ec for sc, ec in zip(c1, extended_c)]
のところで行っています。この書き方を内包表記と言い、c1とextended_cの2つのリストをzipを使って同時に回し、1要素ずつ足し合わせた要素のリストを生成、ということをしています。
あとは足し合わせた血中濃度のリストをreturnで返せば終わりなのですが、ここでCmaxを取得する処理を書いています。
説明する順番が逆になりましたが、メソッドを呼ぶ順番としては①calc_section_concでcmaxを取得しておき、②calc_extended_concで次回投与のための赤いライン部分の血中濃度を計算、ということになります。
インスタンスの生成と描画部分
では上のクラスを使って実際に不均等間隔投与を描画する部分です。
intervals = (8, 16, 24) # 投与間隔をタプルで与える # 不均等でない場合はintervals = (8, )のように書けば良い cycle = 3 # intervalsを何サイクル繰り返すか bc_list = [] conc = [] # 投与間隔毎にインスタンスを生成しリストに加えていく for i, tau in enumerate(intervals): bc_list.append(BloodConc3(x0, vd, k, T, i, tau)) # 延長血中濃度(赤いライン部分)の初期化. 初回投与時は0で良い ex_c = [0 for _ in range(int(intervals[0] / BloodConc3.STEP))] for _ in range(0, cycle): for bc in bc_list: # 単回投与分と延長部分を合わせたものを血中濃度として追加していく conc.extend(bc.calc_section_conc(ex_c)) # 次回投与のために延長部分を計算しておく ex_c = bc.calc_extended_conc(intervals) period = sum(intervals) * cycle time = np.linspace(0, period, num=int(period / BloodConc3.STEP), endpoint=False) plt.plot(time, conc, color='blue', alpha=0.8)
今までnp.linspaceの要素数を指定する部分に時間の刻み幅を0.1や0.01などとハードコーディングしていましたが、今回からクラス変数(インスタンス毎の値ではなくクラスに一つ)の定数として定義することにしています。そして、これを実行した結果がこのページ上部に表示されているグラフとなります。
しかし、このプログラムは投与間隔毎にインスタンスを作る、とか、延長部分の計算する処理を別で呼び出す、などまだまだ改善すべき点が多そうです。
以下、この辺の改良について書きます。
コードを改良する
改善したい点を箇条書きにしてみました。
- 一つのグラフで生成するインスタンスは一つにする
- メソッドは一つ呼ぶだけで血中濃度を計算できるようにしたい
- 投与回によっては投与量も変えられるようにしたい
これらの改善を上のコードから大きくロジックを変えることなくやっていきたいと思います。
class BloodConc4: STEP = 0.01 def __init__(self, x0, vd, k, T, intervals): self.x0 = x0 # タプルで受け取る self.vd = vd self.k = k self.T = T self.intervals = intervals # タプルで受け取る self.idx = 0 # 現在の投与間隔を保持するインデックス self.cmax = 0 self.extended_c = [0 for _ in range(int(intervals[0] / self.STEP))]
インスタンス生成の際に単一の投与間隔と投与量を引数に渡していましたが、投与量と投与間隔を変えられるよう両方ともタプルで渡すことにします。
また、次回投与のための延長分血中濃度もここで0で初期化するように変更します。
次は延長分血中濃度を計算するメソッドです。
# 次回投与間隔分のcを計算しておく def __calc_extended_conc(self): n_idx = (self.idx + 1) % len(self.intervals) # 次回投与間隔のインデックス current_interval = self.intervals[self.idx] # 現在の投与間隔 next_interval = self.intervals[n_idx] # 次回の投与間隔 begin = current_interval - self.T end = begin + next_interval ex_t = np.linspace(begin, end, num=int((end - begin) / self.STEP), endpoint=False) ex_c = self.cmax * np.exp(-self.k * ex_t) self.idx = n_idx return ex_c
大きくは変わっていません。引数をなしにして現在の投与間隔を取得するのにself.idxを使うようにしています。現在の投与間隔は、上でも書いたように今までは単一の値を保持していましたが、タプルで持つようにしたため、beginを求める部分がこのようになっています。また、次回投与のための血中濃度を計算した後に、self.idxを次の投与間隔を示す値に更新しておきます。
次は目的の血中濃度を返す処理です。
# 点滴開始から次回投与までのcを計算する. # 前回投与時の延長分と今回投与分の血中濃度を合計して返す. def calc_section_conc(self): c1 = self.__calc_during_div() c2 = self.__calc_after_div() c1.extend(c2) sum_c = [x + y for (x, y) in zip(c1, self.extended_c)] if self.intervals[self.idx] == self.T: max_pos = int(self.T / self.STEP) - 1 else: max_pos = int(self.T / self.STEP) self.cmax = sum_c[max_pos] # 次回投与のために延長分を計算しておく self.extended_c = self.__calc_extended_conc() return sum_c
ここもほとんど変わりなく、さきほどの延長分の血中濃度を計算するメソッドがreturnの前に入るだけです。
血中濃度計算時の大雑把な処理の流れとしては、
初回投与:1.単回投与分と延長分(0で初期化)の和を計算
2.2回目投与のために次の投与間隔分の濃度を計算
2回目投与:1.単回投与+初回の延長分の和を計算
2.3回目投与のために次の投与間隔分の濃度を計算
・・・
のようになります。
次はインスタンスの生成です。
graphlabel = 'test' # グラフのラベル vd = 30 t_half = 6 k = np.log(2) / t_half T = 1 x0 = (700, 500, 300, 800) # 投与量 intervals = (16, 8, 24, 12) # 投与間隔. 投与量と同じ長さにする cycle = 2 # intervalsを何サイクル繰り返すか bc = BloodConc4(x0, vd, k, T, intervals)
コンストラクタの引数を変えたので、投与量x_0と投与間隔intervalsはタプルで渡していますが、注意点としては、この2つは長さが合っていなくてはいけません。上の例はどちらも長さが4です。次のような書き方でもOKです。
x0 = tuple([400] * 2 + [200] * 6) # 400 x 2, 200 x 6の長さ8 intervals = tuple([12] * 2 + [24] * 6) # 12 x 2, 24 x 6の長さ8
このような書き方であれば、200, 200, 200, ...と同じ投与量(または投与間隔)を繰り返し書く必要がなく、間違いにくいです。
長々と書いてきましたが、ここでいろいろと考えたことが後で2-コンパートメントモデルのテイコプラニンの負荷投与のプログラムを書くときに役に立ちました。
もしご興味があれば、こちらもどうぞ。
www.yakupro.info
今回のコード全文です。
import numpy as np import matplotlib.pyplot as plt # 1-コンパートメント点滴静注モデル. 不均等(間隔・投与量)に対応 class BloodConc4: STEP = 0.01 # 経過時間の刻み幅 def __init__(self, x0, vd, k, T, intervals): self.x0 = x0 # タプルで受け取る self.vd = vd self.k = k self.T = T self.intervals = intervals # タプルで受け取る self.idx = 0 # 現在の投与量、投与間隔を保持するインデックス self.current_interval = intervals[0] self.cmax = 0 self.extended_c = [0 for _ in range(int(intervals[0] / self.STEP))] # 点滴開始~終了直前 def calc_during_div(self): td = np.linspace(0, self.T, num=int(self.T / self.STEP), endpoint=False) c = (self.x0[self.idx] / self.T / self.k / self.vd) * (1 - np.exp(-self.k * td)) return c.tolist() # 点滴終了時~次回投与直前 def calc_after_div(self): ta = np.linspace(0, self.intervals[self.idx] - self.T, num=int((self.intervals[self.idx] - self.T) / self.STEP), endpoint=False) c = (self.x0[self.idx] / self.T / self.k / self.vd) * (1 - np.exp(-self.k * self.T)) * np.exp(-self.k * ta) return c.tolist() # 点滴開始から次回投与までの血中濃度を計算する. # 前回投与時の延長分と今回投与分の血中濃度を合計して返す. def calc_section_conc(self): c1 = self.calc_during_div() c2 = self.calc_after_div() c1.extend(c2) sum_c = [x + y for (x, y) in zip(c1, self.extended_c)] if self.intervals[self.idx] == self.T: max_pos = int(self.T / self.STEP) - 1 else: max_pos = int(self.T / self.STEP) self.cmax = sum_c[max_pos] # 次回投与のために延長分を計算しておく self.extended_c = self.calc_extended_conc() return sum_c # 次回投与間隔分のcを計算しておく def calc_extended_conc(self): n_idx = (self.idx + 1) % len(self.intervals) # 次回投与間隔のインデックス current_interval = self.intervals[self.idx] # 現在の投与間隔 next_interval = self.intervals[n_idx] begin = current_interval - self.T end = begin + next_interval ex_t = np.linspace(begin, end, num=int((end - begin) / self.STEP), endpoint=False) ex_c = self.cmax * np.exp(-self.k * ex_t) self.idx = n_idx return ex_c if __name__ == '__main__': # テスト graphlabel = 'test' vd = 30 t_half = 6 k = np.log(2) / t_half T = 1 x0 = (700, 500, 300, 800) # 投与量 intervals = (16, 8, 24, 12) # 投与間隔. 投与量と同じ長さにする # x0 = tuple([200] * 2 + [200] * 6) # intervals = tuple([12] * 2 + [24] * 6)のような書き方でも可 cycle = 2 # intervalsを何サイクル繰り返すか bc = BloodConc4(x0, vd, k, T, intervals) conc = [] for _ in range(len(bc.intervals) * cycle): conc.extend(bc.calc_section_conc()) period = sum(bc.intervals) * cycle time = np.linspace(0, period, num=int(period / BloodConc4.STEP), endpoint=False) plt.plot(time, conc, color='blue', alpha=0.8, label=graphlabel) plt.ylabel('血中濃度[μg/mL]') plt.xlabel('時間[hr]') plt.xticks(np.arange(0, time[-1] + 24, 24)) plt.xlim(0, ) plt.ylim(0, ) plt.legend() plt.grid(linestyle='dashed') plt.show()