以前1-コンパートメントと2-コンパートメントの静注モデルでもやりましたが、今回は前回記事の1次速度の吸収過程のある1-コンパートメントモデルでやってみようと思います。

血中濃度データの片対数プロット
ある薬物100mgを経口投与後の8点の血中濃度データ*1が得られたとして、これを片対数プロットすると、次の図のようになります。

import numpy as np import matplotlib.pyplot as plt # ある薬物100mgを経口投与後の8点の血中濃度(μg/mL)測定データ t = np.array([0.5, 2.0, 3.5, 6, 8, 10, 20, 30]) # 時間 c = np.array([1.4, 4.3, 5.3, 5.5, 5.1, 4.4, 2.2, 1.1]) # 血中濃度 plt.plot(t, c, 'g.', label='実測値', markersize=9) # 縦軸はログスケール plt.yscale('log', basey=10) # 軸ラベルを表示 plt.xlabel('時間[hr]') plt.ylabel('血中濃度[μg/mL]') # x,y軸の範囲を指定する plt.xlim(0, 40) plt.ylim(1, 15) # グリッドの表示 plt.grid(which='both', linestyle='dashed') # ラベルに応じた凡例を表示 plt.legend() plt.show()
プロットから消失速度定数(ke)と吸収速度定数(ka)を求める
1. 消失速度定数(ke)
ka > keという条件下において、時間がある程度経った場合を考えます。
ここで、=Aとおくと、
この(1)式は以下の消失過程の式で近似できることを前回の記事でみました。
これを常用対数表示にすると、
となります。この式は、上の片対数プロットの最高血中濃度を越えてから濃度が減少していく部分に相当します。この部分の濃度データで直線回帰し、得られた傾きと切片からAとkeを求めることができます。
ではやってみます。
import numpy as np # 8点の血中濃度(μg/mL)の測定データ t = np.array([0.5, 2.0, 3.5, 6, 8, 10, 20, 30]) # 時間 c = np.array([1.4, 4.3, 5.3, 5.5, 5.1, 4.4, 2.2, 1.1]) # 血中濃度 # β相(beta phase)の時間と濃度 bph_time = t[4:8] bph_conc = c[4:8] # 最小二乗法により回帰直線のintercept, slopeを返す def least_squares_method(xdata, ydata): X = np.zeros((len(xdata), 2), float) # データ数×2列の行列を作る X[:, 0] = 1 X[:, 1] = xdata logy = np.log10(ydata) # 血中濃度の常用対数をとる (theta, residuals, rank, s) = np.linalg.lstsq(X, logy, rcond=None) return theta[0], theta[1] # β相の傾きと切片を求める intercept_b, slope_b = least_squares_method(bph_time, bph_conc) # 得られた傾きと切片からke, Aを求める ke = slope_b * -2.303 A = 10 ** intercept_b
まず血中濃度データの後半の4点を使用するため、スライスを使ってt, cから切り出しています。
# β相(beta phase)の時間と濃度 bph_time = t[4:8] bph_conc = c[4:8] print(bph_time) # [ 8. 10. 20. 30.] print(bph_conc) # [5.1 4.4 2.2 1.1]
次に、これらのデータから直線回帰して傾きと切片を求めるのですが、求める関数の
least_squares_method()は以前「バンコマイシンの血中濃度データに2-コンパートメントモデルを当てはめる」で使ったものとまったく同じものを使っています(実際に計算をするのは数値計算ライブラリのnp.linalg.lstsq関数です)。
この関数に先ほど切り出したβ相の時間と濃度データ(bph_timeとbph_conc)を渡してやります。
# β相の傾きと切片を求める intercept_b, slope_b = least_squares_method(bph_time, bph_conc) # 得られた傾きと切片からke, Aを求める ke = slope_b * -2.303 A = 10 ** intercept_b
ここまでが消失速度定数ke, Aを求める部分です。
2. 吸収速度定数(ka)
次は吸収速度定数です。前回の記事で示しましたが、経口投与後の血中濃度Cは二つの指数関数の濃度式C1, C2で表されるのでした。
この最後の式を変形して常用対数をとると、
となり、
さらにと
に上の式を代入して式を整理すると、
となります。この式の左辺の真数部分は『上で求めたβ相の直線上の値-測定した血中濃度の値』のことです。
ではコードに書いていきます。
# α相(alpha phase)の時間と濃度 aph_time = t[:4] # [0.5 2. 3.5 6. ] aph_conc = c[:4] # [1.4 4.3 5.3 5.5] # 消失相(β相)の直線と測定データの差を求める. c_diff = [A * np.exp(-ke * x) - c_data for (x, c_data) in zip(aph_time, aph_conc)]
上式の真数部分を求める処理です。リスト内包表記でzipを使いaph_timeとaph_concから1つずつデータを取り出し、差を求めています。ここでは血中濃度データの前半3点を使いました。あとはこの求めた差のリストと前半3点の時間から直線の傾きを求めます。
と、ここでこれらの点から直線回帰して切片と傾きを求めて・・としたいところですが、keを求めたときの直線と今回引く直線の切片はで同じです。なので、切片は先に求めた
を使い、後は傾きだけを求めます。
y軸方向に切片の値()分平行移動したと考えると、切片0(
が0)の直線の傾きを求めることになります。
最小二乗法で切片が0の直線y=axの傾きaを求める方程式は、
です。これはコードでは
# 切片0(log10A=0)の直線の傾きを求める. slope_a = np.sum(aph_time * (np.log10(c_diff) - intercept_b)) / np.sum(aph_time ** 2)
と書けます。の各データ(リストc_diff)もy軸マイナス方向に平行移動させています。この部分は、np.log10(np.array(c_diff) / A)と書いても同じです。
この直線の傾き(slope_a)から、後はkeのときと同じようにkaを求めます。
# 傾きからkaを求める ka = slope_a * -2.303
結果、A, ka, keは私の環境では次のようになりました。
A: 8.859385463370744, ke: 0.06959043420410074, ka: 0.5249760626239548
これらの値と(1)式を使って、グラフ描画したものがページ上の右図になります。
Scipyのleastsq関数でフィッティング
ここまででパラメータA, ke, kaをグラフから求めることができたので、今度はこれらを初期値として、scipyのleastsq関数を使って非線形最小二乗法を解いてみます。
from scipy import optimize # グラフから得られた値を初期値として1-コンパートメント経口投与モデルの式をフィッティングする. # scipyのoptimize.leastsqを用いて非線形回帰を行い, A, ke, kaを求める # A: 8.859385463370744, ke: 0.06959043420410074, ka: 0.5249760626239548 init_param = [A, ka, ke] print('init_param :', init_param) # パラメータをフィッティングしたい関数を定義する def func(param, t, c): _A = param[0] _ka = param[1] _ke = param[2] return c - _A * (np.exp(-_ke * t) - np.exp(-_ka * t)) result_param = optimize.leastsq(func, init_param, args=(t, c))
既にA, ke, kaは片対数プロットの直線回帰によって得られた値(コメントの値)が入っているものとしています。以前も「バンコマイシンの血中濃度データに2-コンパートメントモデルを当てはめる」で同じようなことをしたので説明は省略しますが、違うのはパラメータをフィッティングしたい関数funcの定義の部分だけです。
注意点として、方程式が=0となるように書くので、returnのところは
と書きます。
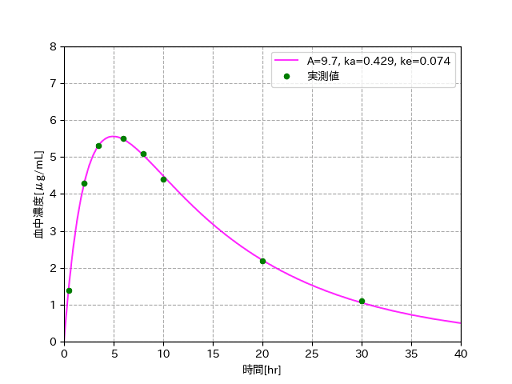
これで求められた値でグラフを描くと下図のようになりました。うまくフィッティングできています。
A: 9.670298588638472, ke: 0.07379740158517506, ka: 0.4292043912218557
ベースにした薬物動態パラメータとの比較
今回の記事で使用した血中濃度データは前回の記事
www.yakupro.info
で描いたグラフから、私が適当に読み取って作ったものです。最終的に求まったパラメータから、一応TmaxとCmaxやその他のパラメータを比較しておきます。
もともとのグラフのパラメータは
| A | ke | ka | Tmax | Cmax |
|---|---|---|---|---|
| 10.4 | 0.08 | 0.4 | 5.03 | 5.57 |
でした。今回求めたパラメータは最終的に
| A | ke | ka | Tmax | Cmax |
|---|---|---|---|---|
| 9.67 | 0.074 | 0.43 | 4.95 | 5.55 |
となりました。初期値は残差法で地道に求めましたが、非線形最小二乗法で使ったscipyのleastsqでより真値に近づきました。残差法で血中濃度データのどこをα相とβ相の区切りとして使うかで初期値が少々変わっても、leastsq関数の結果は変わりませんでした。
ところで、Aはでしたが、keとka, Dを入れてみてもVdを求めるにはFがわからないといけません。本を読んでいると、どうやら経口投与の血中濃度だけではこれを得ることができず、『FとVdのそれぞれを得るには静脈内投与の結果がなければ、得ることができない』(薬物動態解析入門 はじめての薬物速度論)のだそうで、F/Vdはこの形のままの値としてしか求まらないようです。
あと、もう一つ大事なことがあります。今回は最初からka>keということがわかっているものとして話を進めてきました。この条件の場合は消失相(β相)の傾きはkeが反映されますが、ka<keの場合は消失相の傾きはkaが反映されます。
内服モデルの場合は、薬物を経口投与したときの血中濃度データだけではkaとkeのどちらが速いのかがわからず、これらを正確に求めるには、同じ薬物を静注したときのデータが必要になるとのことです。
次回の記事では、このkaとkeの関係について掘り下げて確認してみようと思います。
www.yakupro.info
参考
・統計学入門 14.2 内服モデル
・薬物動態解析入門 はじめての薬物速度論
・徹底解説 薬物動態の数学―微積分と対数、非線形
最後はコード全文です。
import numpy as np import matplotlib.pyplot as plt from scipy import optimize # 血中濃度データに経口投与1-コンパートメントモデルを当てはめる2 # ある薬物100mgを経口投与後の8点の血中濃度(μg/mL)測定データ t = np.array([0.5, 2.0, 3.5, 6, 8, 10, 20, 30]) # 時間 c = np.array([1.4, 4.3, 5.3, 5.5, 5.1, 4.4, 2.2, 1.1]) # 血中濃度 # α, β相で使うデータを先に切り出しておく # β相(beta phase)の時間と濃度 bph_time = t[4:8] bph_conc = c[4:8] print('bph_time: ', bph_time) print('bph_conc: ', bph_conc) # α相(alpha phase)の時間と濃度 aph_time = t[:4] aph_conc = c[:4] print('aph_time', aph_time) print('aph_conc', aph_conc) # 最小二乗法により回帰直線のintercept, slopeを返す def least_squares_method(xdata, ydata): X = np.zeros((len(xdata), 2), float) # データ数×2列の行列を作る X[:, 0] = 1 X[:, 1] = xdata logy = np.log10(ydata) # 血中濃度の常用対数をとる (theta, residuals, rank, s) = np.linalg.lstsq(X, logy, rcond=None) return theta[0], theta[1] # β相の傾きと切片を求める intercept_b, slope_b = least_squares_method(bph_time, bph_conc) # 得られた傾きと切片からke, Aを求める ke = slope_b * -2.303 A = 10 ** intercept_b # [消失相(β相)の外挿した直線上の値 - 測定データ]との差を求める. c_diff = [A * np.exp(-ke * x) - c_data for (x, c_data) in zip(aph_time, aph_conc)] # 切片0(log10A=0)の直線の傾きを求める. slope_a = np.sum(aph_time * (np.log10(c_diff) - intercept_b)) / np.sum(aph_time ** 2) # 傾きからkaを求める ka = slope_a * -2.303 print('片対数プロットの直線回帰による') print('A: {}, ke: {}, ka: {}'.format(A, ke, ka)) # グラフ描画 fig = plt.figure(figsize=(10, 6)) fig.subplots_adjust(wspace=0.3) # plotのためx軸の値を作成 x = np.arange(0, 40, 0.01) # 左側グラフ(片対数プロット) ax1 = fig.add_subplot(1, 2, 1) # (行, 列, プロット番号) # プロットはlogスケールで表示するので変換前の値にしておく alpha_line = np.power(10, intercept_b + slope_a * x) # α相 beta_line = np.power(10, intercept_b + slope_b * (x[int(bph_time[0]*100):])) # β相 beta_exline = np.power(10, intercept_b + slope_b * (x[:int(bph_time[0]*100)])) # β相の外挿(点線)部分 # 各直線のプロット ax1.plot(x, alpha_line, 'red', alpha=0.7, label='A='+str(round(A, 1))+', ka={0:.3f}'.format(ka)) ax1.plot(x[int(bph_time[0]*100):], beta_line, 'blue', alpha=0.7, label='A='+str(round(A, 1))+', ke={0:.3f}'.format(ke)) ax1.plot(x[:int(bph_time[0]*100)], beta_exline, 'blue', alpha=0.7, linestyle='--') # β相の外挿線-実測点のプロット ax1.plot(aph_time, c_diff, '.', color='lime', label='β相の外挿線-実測値', alpha=0.6, markersize=8) ax1.set_yscale('log', basey=10) ax1.set_ylim(0.3, 11) # 右側グラフ(ノーマルプロット) ax2 = fig.add_subplot(1, 2, 2) time = np.arange(0, 40, 0.01) c_form = A * (np.exp(-ke * time) - np.exp(-ka * time)) ax2.plot(time, c_form, color='magenta', label='$A(e^{-ke * t} - e^{-ka * t})$') ax2.set_ylim(0, 8) # 2つのグラフで共通する部分は以下で行う axs = plt.gcf().get_axes() for ax in axs: # 実測データをプロット ax.plot(t, c, '.', color='green', label='実測値', alpha=0.6, markersize=9) # 軸ラベルを表示 ax.set_ylabel('血中濃度[μg/mL]') ax.set_xlabel('時間[hr]') # 横軸の範囲を指定する ax.set_xlim(0, 40) # グリッドの表示 ax.grid(which='both', linestyle='dashed') # ラベルに応じた凡例を表示 ax.legend() plt.show() # グラフから得られた値を初期値として1-コンパートメント経口投与モデルの式をフィッティングする. # scipyのoptimize.leastsqを用いて非線形回帰を行い, A, ke, kaを求める init_param = [A, ka, ke] print('init_param :', init_param) # パラメータをフィッティングしたい関数を定義する def func(param, t, c): _A = param[0] _ka = param[1] _ke = param[2] return c - _A * (np.exp(-_ke * t) - np.exp(-_ka * t)) result_param = optimize.leastsq(func, init_param, args=(t, c)) A = result_param[0][0] ka = result_param[0][1] ke = result_param[0][2] print('非線形最小二乗による解') print('A: {}, ke: {}, ka: {}'.format(A, ke, ka)) D = 100 # 投与量(mg) F_per_Vd = A * (ka - ke) / ka / D print('F/Vd: ', F_per_Vd) # Cmax到達時間 def t_max(_ka, _ke, _lag_time): return np.log(_ka / _ke) / (_ka - _ke) + _lag_time # 最高血中濃度 def c_max(_F, _D, _vd, _ka, _ke): return _F * _D / _vd * (_ka / _ke) ** (_ke / (_ke - _ka)) print('tmax: ', t_max(ka, ke, 0)) print('cmax: ', c_max(F_per_Vd, D, 1, ka, ke)) time = np.arange(0, 40, 0.01) c_form = A * (np.exp(-ke * time) - np.exp(-ka * time)) plt.plot(time, c_form, color='magenta', alpha=0.8, label='A={0:.1f}, ka={1:.3f}, ke={2:.3f}'.format(A, ka, ke)) plt.plot(t, c, 'g.', label='実測値', markersize=9) plt.ylabel('血中濃度[μg/mL]') plt.xlabel('時間[hr]') plt.xlim(0, 40) plt.ylim(0, 8) plt.grid(which='both', linestyle='dashed') plt.legend() plt.show()
*1:参考にした薬などはなく、前回記事のグラフから適当に作った数値です
