薬剤師のプログラミング学習日記

プログラミングやコンピュータに関する記事を書いていきます

トップ > 薬物動態 > バンコマイシンTDM－ベイズ推定プログラムを実装するー

バンコマイシンTDM－ベイズ推定プログラムを実装するー

薬物動態

前回記事では入力された患者情報から母集団PKパラメータを用いてバンコマイシン（VCM）の血中濃度推移をシミュレーションするプログラムを作りました。今回はベイジアン法により対象患者のPKパラメータを推定し、算出されたAUCを基にして推奨投与量を求めるプログラムを作っていきたいと思います。Pythonのバージョン等環境についても前回と同様です。

前置き（と、おことわり）

前回記事と同様に、記事中では参考にした日本化学療法学会のWebアプリケーションであるPATの結果を比較に挙げていますが、今回私が作成したプログラムとはまったく、何の関係もありません。

記事の趣旨としては、Pythonプログラミングによるベイズ推定の実装に主眼を置いています（理論的な部分はやや粗があるかもしれません）。臨床の現場ではTDMソフトを使っているけれど、ベイズ推定についてはよくわかっていない、とかこれから勉強してみたいと思っている薬剤師や学生の方にとって、少しでも理解の助けになるところがあれば幸いです。

TDMにおけるベイズ推定

では本題に入っていきます。

目的

ある患者の特定の投与条件下において、実際に得られたデータ（実測血中濃度）に基づいて薬物動態パラメータ（CLやVd）を推定する、ということが目的になります。

誤差モデルの設定

いくつか前提があるのでそれらについても確認しておきます。

  • 推定したい薬物動態パラメータはある特定の確率分布を持つと仮定します。このPKパラメータが持つ分布やその代表値（平均や分散）は、対象の患者が属する（と想定された）母集団から解析されたものを使用します。

今回のプログラムで使用する母集団PKパラメータも前回同様PATで使用されているものと同じものを使います。

例として、クリアランス(CL)で見てみると、

母集団平均θ 個体間変動η
CL(L/h) θ=0.0478×CCr ω=38.5%

とあります。
CLには個体間変動の要因（共変量）としてCCrを組み込んで平均θを個体ごとに変化させて、個体間変動ηを小さくすることにより予測の精度を高めています。
個体間変動η_{CL}は平均=0、分散=ω^2の正規分布に従うので、値の68%が標準偏差内（ω）に入り、95%がωの2倍以内、99.7%が3倍以内に入ります。

また、各個体のPKパラメータは正の値しか取らず、右に裾を引く形で幅広く分布（対数正規分布）していると考えられることから、指数誤差モデルが適用されることが多くなります。
指数誤差モデルでの個体パラメータCL_{i}は、CL_{pop}を母集団平均とすると、

CL_{i} = CL_{pop} \times \exp(η_{CL})

と表されます。
下図に対数正規分布の確率密度関数*1のプロットと、CCr=83.3mL/minのときの母集団平均CLpop=3.98(L/h)の場合に、指数誤差モデル（青線）と比例誤差モデル（緑線）における各個体が取り得るCLの範囲を示します。

　

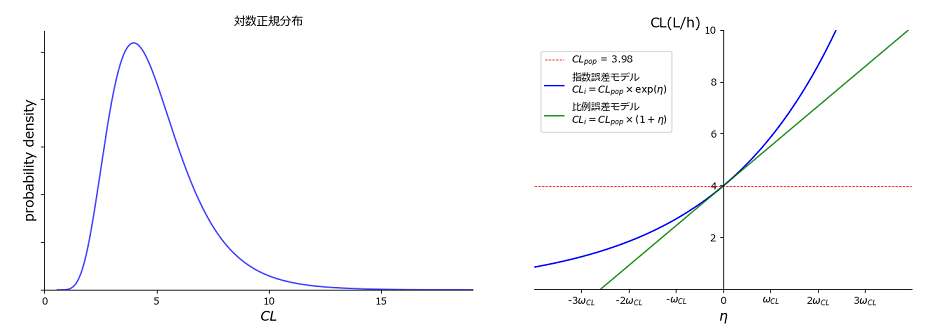
  • PKパラメータの変動が確率分布を持つと仮定したのと同様に、個体内での変動や測定誤差等にも確率分布を仮定します。薬物血中濃度の測定値C_{obs}は、コンパートメントモデルにより推定される薬物血中濃度C_{pred}にこれらの誤差が加わって、実際の測定値となっていると仮定します。このようにすることで、C_{obs}も確率変数として扱うことができます。

このような誤差による変動をまとめて残差変動とし、この誤差を表す確率変数をεとすると、εは平均0、分散 \sigma^2の正規分布に従います。

C_{obs} = C_{pred} \times \exp(ε)

⇔ \log (C_{obs}) = \log (C_{pred}) + ε, \quad ε～N(0, \sigma^2)

このモデルでは、対数スケール上ではどの測定データの誤差項にも同じ正規分布を仮定していますが、元のスケールでは誤差は C_{pred}が大きいほど、 C_{obs}との差が大きくなります。
一般に、薬物血中濃度が高いほど、測定値のばらつきも大きくなる傾向が認められているとのことで、この誤差モデルを設定することにしました。
　

ベイズの定理

では次に実際にどのような計算を行えば良いのかを見ていきます。以前ナイーブベイズというアルゴリズムで文書分類を行う記事を書いたことがありましたが、考え方としては基本的には同じです。
www.yakupro.info

ベイズの定理を再掲します。
D：データ、θ：パラメータとすると

\displaystyle{P(θ|D) = \frac{P(D|θ) ×P(θ)}{P(D)}}

  • P(θ)：事前分布(Prior Distribution)と呼ばれる、データを見る前のθの分布
  • P(θ|D)：事後分布(Posterior Distribution)と呼ばれる、データを見た後のθの分布。つまり、データ観測によって事前分布が修正され得られる分布です。
  • P(D|θ)：尤度(Likelihood)と呼ばれ、パラメータの尤もらしさを表します。
  • P(D)は、どのようなθであってもデータの得られる分布で、周辺尤度(marginal likelihood)と呼ばれます。これは、θに左右されない観測データのみに基づく確率で定数となります。正規化定数とも呼ばれます。

今回のケースでは、データ（実測濃度）を観測した後に個人のCLやVdなどのパラメータを推定したいのでした。つまり、P(θ|D)を最大にするようなθが得られればよいのであって、具体的なP(θ|D)のそのものの値は今回は必要ではありません。従って、P(D)は無視することができ、次の式のように分子の部分だけを評価することになります。*2

\displaystyle{P(θ|D) \propto P(D|θ)P(θ)}

この最適化は最大事後確率（maximum a posteriori：MAP）推定といい、本記事でのTDMにおける「ベイズ推定」や「ベイジアン法」とは、このMAP推定のことを指します。また、この事後確率を最大化させるパラメータをMAP推定量といいます。
次は各項について一つずつみていきます。


・尤度 P(C_{obs}|η)
尤度は与えられた観測データはどのパラメータから最も発生しやすいか、を表します。
前述した条件において、Cobsは次のように表すことができました。

\log (C_{obs})～N(\log (C_{pred}), \sigma^2)

また、ここで C_{pred}はコンパートメントモデルによる血中濃度の予測値ですが、この C_{pred}は当然ηに依存します。（CL, Vdなどはηから算出される値です。）

これらを踏まえた上で、互いに独立な実測血中濃度データCobsがN個与えられたとき、これらN個のデータ点の同時確率分布は次の式のようになります。

\begin{aligned} \small P(C_{obs1}, C_{obs2}, ..., C_{obsN}|η) = \prod\limits_{j=1}^N \dfrac{1}{\sqrt{2\pi\sigma^2}}\exp\left( -\dfrac{\left(\log(C_{obs, j}) - \log(C_{pred, j}(η))\right)^2}{ 2\sigma^2}\right) \end{aligned}

これは正規分布の式と同じですが、データCobsではなくパラメータηの関数であるため尤度関数といい、以下のように明示的にLで表します。
L(η)=\prod\limits_{j=1}^N P(C_{obs_j}|η)

このように同時確率を考えることで、観測されたデータをパラメータに反映させることができます。

・事前分布 P(η)
今回の場合、事前分布は観測データが与えられる前のηの確率分布であり、ηCL, ηVss, ηK21の3つあります。（K12は固定値として扱います）
例としてCLで見ていきます。
η_{CL}～N(0, ω^2)なので、
　
\begin{aligned} \small P(η_{CL}) = \dfrac{1}{\sqrt{2\pi\omega_{CL}^2}}\exp\left( -\dfrac{\left(\eta_{CL} - 0)\right)^2}{ 2 \omega_{CL}^2}\right) \end{aligned}

ここで、個体のパラメータは次のように表されるのでした。

CL_{i} = CL_{pop} \times \exp(η_{CL})

η_{CL} = \log(CL_{i}) - \log(CL_{pop})

これをηCLに代入します。他のηVss、ηK21についても同様です。


・事後分布 P(η|C_{obs})
事後分布は次のように表されます。

\displaystyle{P(η|C_{obs}) \propto P(C_{obs}|η)P(η)}

事後分布を最大化するパラメータを探すことが目標でしたが、次に示す理由から、通常はこの式の対数を取り、さらに-1をかけたものを考えます。

  • 対数を取ると小さな数の積を和とすることができ、扱いやすくなる
  • 対数関数は単調増加であり-1は大小を逆転させるため、最大化問題は最小化問題へ変換することができる

対数を取ると、

\log P(\eta_{CL}, \eta_{Vss}, \eta_{K21} | C_{obs}) = \sum \log L(\eta) + \log P(\eta_{CL}, \eta_{Vss}, \eta_{K21})


最小化の際の極値に影響を与えない部分については無視できる*3ということを踏まえて式を整理して、これを目的関数として表します。*4

\begin{aligned} \mathrm{ Objective\, Function} = {\small \dfrac{\left(\log C_{obs} - \log C_{pred}\right)^2}{\sigma^2} + \dfrac{\left(\log CL_{i} - \log CL_{pop}\right)^2}{\omega_{CL}^2}} \\ {\small + \dfrac{\left(\log Vss_{i} - \log Vss_{pop}\right)^2}{\omega_{Vss}^2} + \dfrac{\left(\log K21_{i} - \log K21_{pop}\right)^2}{\omega_{K21}^2}} \end{aligned}


ある患者の実際に得られたデータ（実測血中濃度）から、薬物動態パラメータ（CLやVd）を推定するという問題は、ベイジアン法によって、この目的関数を最小化するパラメータηを探すという問題に帰着しました。
コードでは関数名はobjective()とし、与えられたηから関数内でPKパラメータを算出し、それを基に生成したインスタンスでC_pred（予測血中濃度）の計算を行います。デフォルト引数にlam（λ）がありますが、これについては後述します。

def objective(params, *args, lam=1.5):
    eta_cl, eta_v, eta_k21 = params
    CL_pop, Vss_pop, K21_pop, K12_fixed = args[0]
    omega_CL, omega_Vss, omega_K21, sigma = args[1]
    dosage = args[2]
    obs_times, c_obs = args[3:]
 
    CL_i = CL_pop * np.exp(eta_cl)
    Vss_i = Vss_pop * np.exp(eta_v)
    K21_i = K21_pop * np.exp(eta_k21)
 
    param_i = [CL_i, Vss_i, K21_i, K12_fixed]
    model = TwoCompInfModel(*param_i, **dosage)
    # log prior
    term1 = np.log(CL_i / CL_pop) ** 2 / omega_CL ** 2
    term2 = np.log(Vss_i / Vss_pop) ** 2 / omega_Vss ** 2
    term3 = np.log(K21_i / K21_pop) ** 2 / omega_K21 ** 2
    # log likelihood
    obs_value = 0
    for c, obs_t in zip(c_obs, obs_times):
        c_pred = model.get_conc_at_time(obs_t)
        obs_value += np.log(c / c_pred) ** 2 / sigma ** 2
    return obs_value + lam * (term1 + term2 + term3)

　

実測濃度情報の入力

お手本としたPATではベイズ推定を行う際には「実測濃度(μg/mL)、採血タイミング、n回投与後」の3項目を入力します。作成するプログラムでも同様の方式にしたいと思います。
これら3項目をタプルとしたリストで与えると、投与開始後の実測血中濃度を得た時間とその濃度に変換し、目的関数と共に最適化ソルバーに渡します。
例えば、4回投与後（5回直前）のトラフの実測濃度が18μg/mL、5回投与後の投与終了1時間後のピーク濃度が35μg/mLの場合は以下のように与えます。

# 実測血中濃度情報の入力
# (実測濃度(μg/mL)、採血タイミング、n回投与後)
cobs_info = [
    (18, 'trough', 4),
    (35, 'c1', 5)
]
# pop_modelは母集団平均のインスタンス
obs_times, c_obs = create_cobs_info_list(pop_model, cobs_info)    
print('obs_times, c_obs', obs_times, c_obs)  #  [44, 46.0] [18, 35]

「c1」の意味は「投与終了1時間後」という意味です。もちろん「c1.5」や「c2」でもOKです。このへんの仕様もPATのルールに倣いました。
関数create_cobs_info_list()は与えられたn回投与後の'trough'や'c1'等の文字列を投与開始後の経過時間に変換する関数です。例えば、投与間隔が[8, 12, 12, 12, 12]で2回目以降の点滴時間が1時間のとき、4回目投与後の'trough'なら44(hr)、5回目投与後の'c1'なら46(hr)、といった具合です。

Scipyによる目的関数の最小化

最小化すべき目的関数は決まりましたが、2-コンパートメントモデルは薬物動態パラメータに関して非線形で、解析的にこれを求めることができません。今回はこの非線形最適化を解くためにScipyのoptimize.minimize()を使いました。

def calc_bounds(omegas, multiplier=3):
    return [(-omega * multiplier, omega * multiplier) for omega in omegas]
 
# 個体間変動(標準偏差)
omega_CL = 0.385
omega_Vss = 0.254
omega_K21 = 0.286
 
# 個体内変動(標準偏差)
sigma = 0.237
 
variability = [omega_CL, omega_Vss, omega_K21, sigma]
initial_eta = [0, 0, 0]
multiplier = 3  # -multiplier * SD < omega < multiplier * SD
bounds = calc_bounds([omega_CL, omega_Vss, omega_K21], multiplier)
 
result = minimize(objective,
              initial_eta,
              method='Powell',
              bounds=bounds,
              args=(params, variability, dosage, obs_times, c_obs))

いろいろ試してみましたが、最終的には最適化手法（method）には'Powell'を使うことにしました。勾配（微分）が不要というのが大きかったですが、'Nelder-Mead'に比べて若干速いかなというのと、僅かながら結果がPATに近いかなと思ったことが理由です。また、ηの初期値は0として、変数の境界制約（bounds）は±3標準偏差以内とすることにしました。

AUCガイドによる推奨投与量の計算

ベイズ推定によりηの推定値が得られた後、それらの値からPKパラメータのCL、Vss、K21を算出してモデルを再構築します。この推定モデルにおける、目標AUCに対する１日投与量は以下の式を使って求めます。AUCは投与量に対して線形なので、比例計算で求めることができます。

\displaystyle{ \text{推奨1日投与量} = \text{現在の1日投与量} \mathrm{\times \dfrac{目標AUC}{推定モデルのAUC}}}

目標AUCは今回は500μg h/mLに設定します。
推奨投与量が求まったとして、次に投与回数についてですが、1回投与量が低くなる（＝腎機能が悪い）ような症例ではわざわざ２回に分ける必要はないだろうということから、今回は単純に１日投与量が800mgより大きい場合に1日2回投与になるようにしました。

テスト症例による実行結果

では実際にプログラムを動かしてみます。テストはPATのマニュアルにあった例で試してみました。
バンコマイシンTDMソフトウェア PAT｜委員会報告・ガイドライン｜公益社団法人日本化学療法学会

・症例：60歳 男性、体重 60 kg、血清クレアチニン値 0.8 mg/dL
・投与計画：初回負荷量として 25mg/kg（1.5時間div）、その8時間後から維持量として1回15 mg/kg（1時間div）を12時間ごと
・血中濃度測定：5回目投与直前に 18 μg/mL、5回目投与終了後1時間後に35 μg/mL

実測濃度情報の入力は上の項目で示した通りです。患者背景と投与条件の入力方法につきましては、前回記事に詳しく書きましたので、よろしければご参照ください。
www.yakupro.info

上記の患者背景、投与条件、実測濃度2点をコード中に書いてからプログラムを実行すると、まず最初は母集団平均による時間-濃度プロファイルが描画されます。
グラフ右下に"Bayesian estimation"のボタンを作成しているので、これをクリックすると目的関数の最小化を実行し、ベイズ推定PK値によるグラフ描画や投与量(AUC for 500)の計算が行われます。

以下に結果を示します。（画像はページトップと同じ）

Estimated eta_cl: -0.27272876087805287
Estimated eta_v: 0.019757024362795313
Estimated eta_k21: 0.028380824189839123
Estimated CL: 3.031 L/h
Estimated Vss: 61.911 L
Estimated K21: 0.219 L/h
 message: Optimization terminated successfully.
 success: True
  status: 0
     fun: 1.097042474191352
       x: [-2.727e-01  1.976e-02  2.838e-02]
     nit: 2
   direc: [[ 0.000e+00  0.000e+00  1.000e+00]
           [ 0.000e+00  1.000e+00  0.000e+00]
           [ 7.801e-04 -6.395e-05 -8.108e-05]]
    nfev: 112

funは最小化された目的関数の値（Objective function value）で、xはそのときの各パラメータetaの値です。ちなみに、PATでベイズ推定の際にグラフ右上に表示される”OFV”とはおそらくこのfunのことですね。今回のプログラムでも同様に表示されるようにしました。
nit（Number of iterations）はオプティマイザが実行した反復回数、direc（direction matrix）はPowellが使用した探索方向、nfev（Number of function evaluations）は目的関数が評価された回数です。（今回はオプティマイザがPowellなので、njevやnhevは表示されません。）
　
今回たまたまかもしれませんが、ベイズ推定PK値はPATの結果とほとんど同じ値となりました。したがって、投与量（for AUC 500）もだいたい同じですが、計算アルゴリズムの違いからかPATは800mg 1日2回なのに対して私のプログラムでは750mg 1日2回という結果になりました。
どちらにしても、一旦推定PK値が出ればAUCは簡単に計算できるので、症例に応じてAUCを取るか調剤しやすい量を取るかを考慮して調整しても良いですね。

事前分布を使う意味

今回導出された目的関数の尤度の項は実測とモデルによる予測の差（誤差）の大きさを返します。ということは、予測と実測が近ければ近いほど、目的関数の値は小さくなります。また、事前分布の項はCL等の個人のPKパラメータが平均に近ければ近いほど、目的関数の値は小さくなり、反対に離れれば離れるほど、目的関数の値は大きくなります。
　
目的関数を最小化するパラメータηとは、尤度の項についてみれば実測値に沿ったシミュレーションカーブを描けるような、平均からは離れたパラメータが良いわけですが、そうすると今度は事前分布の項が大きくなってしまい最小化からは遠ざかってしまいます。
これは見方を変えると、事前分布の項があることでパラメータが極端な値を取ることにブレーキをかけていることになります。

もし事前分布（=正則化項）がなかったら

下に事前分布の項がない場合に、実測値に対してどのようにフィッティングが変わるかを試した図を載せます。
なお、ここでは「極端な値」の例として、先ほどのテスト例の実測値が2点とも+5μ/mLだったとして実験を行っています。

上図が事前分布ありの場合、下図が事前分布なしの場合の最適化の結果です。
下図では実測データに対して過剰適合（オーバーフィッティング）していることが見て取れます。*5
MAP推定は最尤推定（尤度関数だけを使った推定）に過学習を防ぐための工夫である正則化を加えたものとみることができます。正則化については、以前記事で書いたことがありますのでよろしければご参照ください。
www.yakupro.info

正則化パラメータのチューニング

実測値にうまくフィットすることと、PKパラメータが極端な値を取らないというレードオフをコントロールするために、作成したobjective関数ではデフォルト引数として正則化パラメータλを導入しています。適度にデータにも適合し、かつ過学習にならない、ほどほどの地点を探ることになります。この値を大きくすればパラメータηは平均（＝0）に近づくことになり、最小化を実行しても値はほとんど動くことはありません。
下図にλ=500の例を示します。

いろいろ試した結果、今回のプログラムではλ=1.5とすることにしました。


2-コンパートメントモデルは複数の変数から成る複雑な関数です。このような複雑な関数を、実測値1点でフィッティングするにはモデルの表現力に対して、データの数が少なすぎるわけですね。
反対に実測データの数が多ければどうかを考えてみます。
実測データの数が多ければ、目的関数の最小化には尤度の寄与が大きくなり、平均から離れた値でも取りやすくなります。したがって、実測データが新しく得られるたびに対象患者個人のパラメータであるという確実性が更新されていくということが言えます。しかし、単に実測データが多ければそれで良いのかというと、そうではありません。

採血タイミングが推定に与える影響

採血タイミングがトラフなのかピークなのかによって*6血中濃度が持つ情報には違いがあり、推定PK値にもそれが反映されます。

ピーク値は投与後の早い時間の血中濃度です。つまり薬物の初期の体内分布の濃度であるため、Vdの情報が得られます。一方トラフ値は投与直前、多くの薬物が体内から排出された後の血中濃度であるためCLの情報が得られます。反対に、Vdに関する情報は少なくなります。（少ないと言っても、含まれていないわけではありません）

どちらか一方だけの採血タイミングでは、Vd、CL両方のパラメータを正確に推定することは無理があるということです。上でも書きましたが、複雑なモデルであるため異なる時間点の実測データが複数あることでより推定PK値の正確さが高まる、と考えて良いかと思います。
推定するのに情報が不足しているPK値は、結局事前分布に依存した推定値（＝母集団平均に近い値）となり、患者個別の情報を反映した結果とは言えなくなります。

TDMソフトのベイズ推定を使う上で薬剤師が知っておきたいこと

まとめになります。

  • 事前分布は結果に大きな影響を与えています。対象患者が事前分布（母集団）から大きく離れていると思われる場合には、そのことを踏まえておく必要があります。
  • トラフ値だけでなくピーク値も用いた2点で推定を行う方がAUC算出の正確性は高まります。トラフ値からだけの推定を行う場合は、算出されるAUCには2点推定よりも大きな誤差が含まれる場合があることを考慮しておかなければなりません。

　

参考

クリニカルファーマコメトリクス

クリニカルファーマコメトリクス

  • 南山堂
Amazon
・母集団薬物デ-タの解析 (統計科学選書 6)
・月刊薬事2022年05月号 [雑誌] (特集:抗菌薬TDM臨床実践ガイドライン2022はここに注目! 新旧抗菌薬の使い方)


最後に今回作成したプログラムを載せておきます。苦労した所も多かったですが、作る過程そのものや、作ったプログラムを使っていろいろと実験することで見えてきた部分も多く、私自身の中では意味のある取り組みだったと思います。

import matplotlib.pyplot as plt
import matplotlib.widgets as wg
import numpy as np
from decimal import Decimal, ROUND_HALF_UP
from scipy.integrate import trapezoid
from scipy.optimize import minimize
 
 
class TwoCompInfModel:
    STEP = 60     # 濃度プロファイルの時間単位を定義　1hr/60STEP=1min/step
    FACTOR = 10   # 半減期の何倍まで計算するか
 
    def __init__(self, *params, **kwargs):
        self.CL, self.Vss, self.K21, self.K12 = params
        self.Vd1 = self.Vss / (1 + self.K12 / self.K21)
        self.K10 = self.CL / self.Vd1
 
        x = self.K12 + self.K21 + self.K10
        y = self.K21 * self.K10
        self.alpha = 0.5 * (x + np.sqrt(x ** 2 - 4 * y))
        self.beta = x - self.alpha
        self.half_life = 0.693 / self.beta  # np.log(2) / self.beta
 
        tau_times_cycle = sum([x[2] * x[3] for x in kwargs.values()])  # dosage毎のtau*numの合計
        self.period = int(tau_times_cycle + self.half_life * self.FACTOR)
        self.conc = np.zeros(self.period * self.STEP)
        self.time = np.linspace(0, self.period, self.period * self.STEP, endpoint=False)
        self.total_n = 0  # 投与回数を保持
        self.tau_list = []
        self.inf_t_list = []
        self.create_dosing_conditions_list(kwargs)
        self.calc_conc(kwargs)
 
    def create_dosing_conditions_list(self, dosage):
        for d in dosage.values():
            _, inf_t, tau, cycle = d
            self.tau_list += [tau for _ in range(cycle)]
            self.inf_t_list += [inf_t for _ in range(cycle)]
        self.tau_list = np.array(self.tau_list)
        self.inf_t_list = np.array(self.inf_t_list)
 
    def calc_conc(self, dosage):
        for d in dosage.values():
            self.dose, self.T, self.tau, self.cycle = d
            self.calc_exp_coeff()
            self.calc_overlapping_conc()
 
    def calc_exp_coeff(self):
        K0 = self.dose / self.T
        self.A = (K0 * (self.K21 - self.alpha)) / (self.Vd1 * self.alpha * (self.beta - self.alpha))
        self.B = (K0 * (self.K21 - self.beta)) / (self.Vd1 * self.beta * (self.alpha - self.beta))
 
    def calc_during_inf(self):
        t = np.linspace(0, self.T, num=int(self.T * self.STEP), endpoint=False)
        return self.A * (1 - np.exp(-self.alpha * t)) + self.B * (1 - np.exp(-self.beta * t))
 
    def calc_post_inf(self, begin, end):
        t = np.linspace(begin, end, num=int((end - begin) * self.STEP), endpoint=False)
        return self.A * (np.exp(-self.alpha * (t - self.T)) - np.exp(-self.alpha * t)) \
               + self.B * (np.exp(-self.beta * (t - self.T)) - np.exp(-self.beta * t))
 
    def calc_single_dose_conc(self):
        c1 = self.calc_during_inf()
        c2 = self.calc_post_inf(self.T, self.half_life * self.FACTOR)
        c = np.concatenate([c1, c2], axis=0)
        return c
 
    def calc_overlapping_conc(self):
        c = self.calc_single_dose_conc()
        length = len(c)
        loop_cnt = 0
        for i, _ in enumerate(self.tau_list, self.total_n):
            elapsed_time = np.sum(self.tau_list[:i])
            start_idx = int(elapsed_time * self.STEP)
            end_idx = start_idx + length
            self.conc[start_idx:end_idx] += c
            loop_cnt += 1
            if loop_cnt == self.cycle:
                self.total_n += self.cycle
                break
 
    def get_conc(self):
        return self.conc, self.time
 
    def get_cl(self):
        return self.CL
        # CL = Dose / AUC
        # return self.dose / ((self.A + self.B) * self.T)
 
    def get_cmax(self):
        # トラフ値textの座標取得のため
        return np.max(self.conc)
 
    def get_trough(self, num_doses):
        # 指定された投与回数のトラフ値を返す. 範囲を超える場合は最後のトラフを返す
        elapsed_time = np.sum(self.tau_list[:num_doses])
        return self.conc[int(elapsed_time * self.STEP)]
 
    def calc_auc(self):
        # AUC = Dose / CL
        return self.dose / self.CL * 24 / self.tau
 
    def calc_auc_mic_ratio(self, mic=1):
        return self.calc_auc() / mic
 
    def calc_trapezoidal_auc(self, begin, end):
        begin *= self.STEP
        end *= self.STEP
        auc = trapezoid(self.conc[begin:end])
        return auc / self.STEP
 
    def calc_trapezoidal_auc_org(self, begin, end, N=1000):
        begin *= self.STEP
        end *= self.STEP
        h = (end - begin) / N
        s = 0
        for k in range(1, N):
            s += self.conc[begin + int(k * h)]
        s *= h
        s += h * (self.conc[begin] + self.conc[end]) * 0.5
        return s / self.STEP
 
    def calc_css_trough(self, t_const=1.7):
        css_range = self.half_life * self.FACTOR * t_const
        c = self.calc_post_inf(self.T, css_range)
        n = css_range // self.tau
        tr_idx = (np.arange(1, n) * self.tau - self.T) * self.STEP
        return np.sum(c[tr_idx.astype(np.int32)])
 
    def get_conc_at_time(self, time_hr):
        return self.conc[int(time_hr * self.STEP)]
 
    def convert_timing_to_hours(self, timing, num_doses=0):
        # Note: num_dosesは全投与回数を超えないように
        if type(timing) is str:
            if timing.casefold() == 'trough':
                return np.sum(self.tau_list[:num_doses])
            else:
                t = float(timing[1:])  # delete 'c'
                time = np.sum(self.tau_list[:num_doses - 1]) + \
                       self.inf_t_list[num_doses - 1] + t
                return time
        return float(timing)
 
    def calc_tdd_for_auc500(self):
        # total daily dose for auc 500
        return self.dose * 24 / self.tau * 500 / self.calc_auc()
 
 
def create_cobs_info_list(TwoCompInfModel, arg):
    obs_times, c_obs = [], []
    for info in arg:
        c, timing, n_doses = info
        t = TwoCompInfModel.convert_timing_to_hours(timing, n_doses)
        obs_times.append(t)
        c_obs.append(c)
    return obs_times, c_obs
 
 
def calc_bounds(omegas, multiplier=3):
    return [(-omega * multiplier, omega * multiplier) for omega in omegas]
 
 
def objective(params, *args, lam=1.5):
    eta_cl, eta_v, eta_k21 = params
    CL_pop, Vss_pop, K21_pop, K12_fixed = args[0]
    omega_CL, omega_Vss, omega_K21, sigma = args[1]
    dosage = args[2]
    obs_times, c_obs = args[3:]
 
    CL_i = CL_pop * np.exp(eta_cl)
    Vss_i = Vss_pop * np.exp(eta_v)
    K21_i = K21_pop * np.exp(eta_k21)
 
    param_i = [CL_i, Vss_i, K21_i, K12_fixed]
    model = TwoCompInfModel(*param_i, **dosage)
    # log prior
    term1 = np.log(CL_i / CL_pop) ** 2 / omega_CL ** 2
    term2 = np.log(Vss_i / Vss_pop) ** 2 / omega_Vss ** 2
    term3 = np.log(K21_i / K21_pop) ** 2 / omega_K21 ** 2
    # log likelihood
    obs_value = 0
    for c, obs_t in zip(c_obs, obs_times):
        c_pred = model.get_conc_at_time(obs_t)
        obs_value += np.log(c / c_pred) ** 2 / sigma ** 2
    return obs_value + lam * (term1 + term2 + term3)
 
 
def find_closest_dose(target):
    dose_list = [x for x in range(400, 4000, 100)]
    return min(dose_list, key=lambda x: abs(x - target))
 
 
def round_v(f, digits='0.01'):
    return str(Decimal(str(f)).quantize(Decimal(digits), ROUND_HALF_UP))
 
 
def disp_trough(TwoCompInfModel, ax, add_pos=0, color='black'):
    margin = 7
    for i, t in enumerate(TwoCompInfModel.tau_list[:-1], 1):
        etime = sum(TwoCompInfModel.tau_list[:i])
        ax.text(etime - 2, TwoCompInfModel.get_cmax() + margin + add_pos,
                round_v(TwoCompInfModel.get_trough(i)), color=color)
 
 
def disp_text(TwoCompInfModel, ax, add_pos, situation, color='black'):
    ax.text(0, 1.21 + add_pos, 'First   0-24hr AUC: ' +
            round_v(TwoCompInfModel.calc_trapezoidal_auc(0, 24)) + ' μg h/mL',
            transform=ax.transAxes, color=color)
    ax.text(0, 1.16 + add_pos, 'First 24-48hr AUC: ' +
            round_v(TwoCompInfModel.calc_trapezoidal_auc(24, 48)) + ' μg h/mL',
            transform=ax.transAxes, color=color)
    ax.text(0.27, 1.21 + add_pos, situation + ' PK値: ' +
            'CL=' + round_v(TwoCompInfModel.get_cl()) + ' L/h, ' +
            'Vd=' + round_v(TwoCompInfModel.Vss) + ' L, ' +
            '半減期=' + round_v(TwoCompInfModel.half_life) + ' hr, ' +
            'AUC=' + round_v(TwoCompInfModel.calc_auc()) + ' μg h/mL, ' +
            'トラフ値=' + round_v(TwoCompInfModel.calc_css_trough()) + ' μg/mL',
            transform=ax.transAxes, color=color)
 
 
def disp_new_dose_text(TwoCompInfModel, ax, new_dose, n_doses, color='purple'):
    ax.text(0.27, 1.06,
            '●ベイズ推定 投与量 (for AUC 500): ' +
            round_v(new_dose, '1') + ' mg, ' +
            round_v(24 / n_doses, '1') + ' h 毎に, ' +
            'AUC=' + round_v(TwoCompInfModel.calc_auc()) + ' μg h/mL, ' +
            'トラフ値=' + round_v(TwoCompInfModel.calc_css_trough()) + ' μg/mL',
            transform=ax.transAxes, color=color)
 
 
def plot_conc(TwoCompInfModel, ax, color='blue'):
    conc, time = TwoCompInfModel.get_conc()
    ax.plot(time, conc, alpha=0.8, linewidth=0.8, color=color)
 
 
def set_format(TwoCompInfModel, ax, ccr, egfr, warning, dosage):
    margin = 7
    ax.text(0, 1.29, 'Result', fontsize=21, transform=ax.transAxes)
    ax.text(0.27, 1.27, 'Model: Vancomycin (Adult) ', fontsize=12, transform=ax.transAxes)
    ax.text(0.50, 1.27,
            'CCr=' + round_v(ccr, '0.1') + ' mL/min,  ' +
            'eGFR=' + round_v(egfr, '0.1') + ' mL/min/1.73m$^{2}$',
            transform=ax.transAxes)
    ax.text(0, TwoCompInfModel.get_cmax() + margin, 'Trough')
    ax.set_ylabel('Concentration(μg/mL)')
    ax.set_xlabel('Time after dose(hr)')
    ax.set_xticks(np.arange(0, TwoCompInfModel.time[-1] + 12, 12))
    ax.hlines(10, -12, TwoCompInfModel.time[-1], color='red', linewidth=0.8)
    ax.hlines(20, -12, TwoCompInfModel.time[-1], color='red', linewidth=0.8)
    ax.tick_params(width=2, length=5)
    ax.set_xlim(-3, TwoCompInfModel.period - TwoCompInfModel.half_life * 7)
    ax.set_ylim(-3, TwoCompInfModel.get_cmax() + 15)
    ax.text(0, -0.2, '<投与歴>', transform=ax.transAxes)
    for i, d in enumerate(dosage.values()):
        dose, inf_t, tau, n = d
        dosage = f'{i+1}. Dose: {dose:4},  Inf_time: {inf_t:3}, Tau: {tau:3}, N: {n:2}'
        ax.text(0, -0.25 - i * 0.05, dosage, transform=ax.transAxes)
    if warning:
        ax.text(0.50, 1.33, 'Warning: Renal function estimation may be inaccurate.',
                transform=ax.transAxes, fontsize=11, color='red')
 
 
def calc_vancomycin_cl(sex, age, weight, scr, muscle_wasting):
    f = 0.85 if sex == 'female' else 1.0
    ccr = ((140 - age) * weight) / (72 * scr) * f  # Cockcroft-Gault
    ccr = float(round_v(ccr, '0.1'))  # PATはここで丸めてる
    if muscle_wasting and ccr > 85:
        print("Renal function estimation may be inaccurate. ")
        cl = 3.51
    else:
        cl = 0.0478 * ccr
    return ccr, cl
 
 
def calc_egfr(sex, age, scr):
    f = 0.739 if sex == 'female' else 1.0
    return 194 * scr ** -1.094 * age ** -0.287 * f
 
 
if __name__ == '__main__':
    # 患者情報の入力
    age = 60
    weight = 60
    scr = 0.8
    sex = 'male'  # 'male' or 'female'
    muscle_wasting = False  # 著明な筋肉量低下があるか
    scr_round_up = False    # Scr<0.6の場合にScr=0.6とする補正を行うか
    scr = 0.6 if scr_round_up and scr < 0.6 else scr
 
    ccr, CL_pop = calc_vancomycin_cl(sex, age, weight, scr, muscle_wasting)
    egfr = calc_egfr(sex, age, scr)
 
    # PATで使用されているものと同じ母集団薬物動態パラメータを使用
    Vss_pop = 60.7     # Vss = Vd1 + Vd2 = (1 + k12 / k21) * Vd1
    K12_fixed = 0.525  # 中央→抹消コンパートメントへの消失速度定数(/hr)
    K21_pop = 0.213    # 抹消→中央コンパートメントへの消失速度定数(/hr)
 
    params = [CL_pop, Vss_pop, K21_pop, K12_fixed]
 
    # 投与条件の設定. 不均等投与に応じてdosageを作成
    # [投与量(mg), 点滴時間(hr), 投与間隔(hr), 投与回数]
    dosage = {
        'd1': [1500, 1.5, 8, 1],
        'd2': [900, 1, 12, 4]
    }
 
    pop_model = TwoCompInfModel(*params, **dosage)
 
    fig = plt.figure(figsize=(12.5, 7))
    fig.subplots_adjust(right=0.95, left=0.08, top=0.75, bottom=0.22)
    ax = fig.add_subplot(111)
 
    set_format(pop_model, ax, ccr, egfr, muscle_wasting, dosage)
    plot_conc(pop_model, ax)
    disp_trough(pop_model, ax)
    disp_text(pop_model, ax, 0, '〇母集団平均')
    ax2 = fig.add_axes([0.8, 0.05, 0.15, 0.075])
    button = wg.Button(ax2, 'Bayesian estimation')
 
    # 実測濃度情報の入力
    # - observed conc value
    # - blood collection timing ('trough', 'c1', 'c1.5',... , or hour)
    # - num of doses,
    cobs_info = [
        (18, 'trough', 4),
        (35, 'c1', 5)
    ]
 
    obs_times, c_obs = create_cobs_info_list(pop_model, cobs_info)
    print('obs_times, c_obs', obs_times, c_obs)
 
    # 個体間変動(標準偏差)
    omega_CL = 0.385
    omega_Vss = 0.254
    omega_K21 = 0.286
 
    # 個体内変動(標準偏差)
    sigma = 0.237
 
    variability = [omega_CL, omega_Vss, omega_K21, sigma]
    initial_eta = [0, 0, 0]
 
    def button_click(event):
        multiplier = 3  # -multiplier * SD < omega < multiplier * SD
        bounds = calc_bounds([omega_CL, omega_Vss, omega_K21], multiplier)
        result = minimize(objective,
                          initial_eta,
                          method='Powell',
                          bounds=bounds,
                          args=(params, variability, dosage, obs_times, c_obs))
        eta_cl_est, eta_v_est, eta_k21 = result.x
        minimized_ofv = result.fun
        # 最適化されたパラメータを使って血中濃度のグラフを描画
        CL_est = CL_pop * np.exp(eta_cl_est)
        Vss_est = Vss_pop * np.exp(eta_v_est)
        K21_est = K21_pop * np.exp(eta_k21)
 
        print(f"Estimated eta_cl: {eta_cl_est}")
        print(f"Estimated eta_v: {eta_v_est}")
        print(f"Estimated eta_k21: {eta_k21}")
        print(f"Estimated CL: {round_v(CL_est, '0.001')} L/h")
        print(f"Estimated Vss: {round_v(Vss_est, '0.001')} L")
        print(f"Estimated K21: {round_v(K21_est, '0.001')} L/h")
        print(result)
 
        est_params = [CL_est, Vss_est, K21_est, K12_fixed]
        est_model = TwoCompInfModel(*est_params, **dosage)
 
        for obs_time, obs in zip(obs_times, c_obs):
            ax.scatter(obs_time, obs, color='black')
        ax.text(0.99, 0.99, 'OFV=' + round_v(minimized_ofv),
                transform=ax.transAxes, ha='right', va='top')
 
        color = 'green'
        plot_conc(est_model, ax, color)
        disp_trough(est_model, ax, -7, color)
        disp_text(est_model, ax, -0.1, '●ベイズ推定', color)
        # AUC 500のための投与量を計算
        new_dose = est_model.calc_tdd_for_auc500()
        n_doses = 2 if new_dose > 800 else 1
        tau = 24 / n_doses
        new_dose = find_closest_dose(new_dose) / n_doses
        new_dosage = {'new_dosage': [new_dose, 1, tau, 2]}
        new_vcm = TwoCompInfModel(*est_params, **new_dosage)
        disp_new_dose_text(new_vcm, ax, new_dose, n_doses)
        fig.canvas.draw()
 
 
    button.on_clicked(button_click)
    plt.show()

*1:確率密度（probability density）とは、ある範囲内の値を取る確率がどれくらい高いかを示したものです

*2:記号∝は比例関係を表します

*3:実際には最適化アルゴリズムの特性やスケーリングの影響によって異なる結果が生じることがあるようです

*4:式が長くなるので尤度の項のシグマは除いています

*5:OFVも0.00となっています

*6:より正確に言うと、投与後の経過時間によって