主成分分析(PCA:Principal Component Analysis)では、データの本質的な部分に注目して重要な部分を保持し、あまり重要でない部分を削る、一言でいえばデータの要約(=次元削減)を行います。いろいろな分野で使われている手法ですが、機械学習においては与えられたデータから自動的にこの要約を行うため、教師なし学習に分類されます。
PCAを行うメリット
主に次のようなものがあげられます。
・データが持っている情報の本質的な部分を保ったまま、メモリ消費や保存容量を抑えることができる。
・高次元のデータセットを2次元、3次元まで下げることで可視化したり、少数の主成分で表現することによって人間にとってよりわかりやすいデータにすることができる。
・データを新しい表現にしてから学習することで、機械学習アルゴリズムの精度が向上したり学習のスピードを上げることができる。一方で、削られる情報によっては性能が下がってしまうこともあるため、 試行錯誤が必要になる。
PCAの視覚的なイメージ
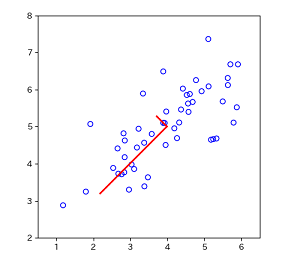
2次元のデータを1次元に削減した場合を可視化してみます。
PCAでは、まず最も分散が大きい方向(=データが最も情報を持っている方向:図中長い赤線)を見つけます。この方向のことを「主成分」と呼び、この最初の主成分を第1主成分といいます。次に、この第1主成分と直交する軸*1の中から最も情報を持っている方向(短い赤線)を探します。
簡単に言うと、これらの主成分はデータの特徴をよりよく掴んだ新たな座標軸である、と言えます。また、主成分は元のデータがn次元ならn個存在します。
この主成分のいくつかだけを残すことで、次元削減を行うことができます。
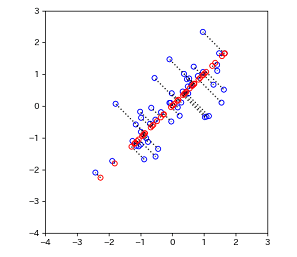
この場合は最初の主成分だけを残すことで、元々2次元だったデータを次のような1次元のデータに削減することができます。大雑把な言い方ですが、この1次元の表現でも元々のデータの情報の大事なところはだいたい表現できている、と考えられます。
[ 1.49631261 -0.92218067 1.22439232 ... -1.44264131]
![]()
なお、ここでは「削減」という表現を用いていますが、単純にもともとの特徴量のうちの1つだけを残したのではなく、新しい軸(第1主成分)を見つけて、そこに各データの特徴量を写すことで次元を「削減」するという意味です。「圧縮」や「縮約」と表現されることもあるようです。
次は3次元データを2次元に削減する場合を見てみます。
以下のようなZ軸方向にはあまり広がっていない、少し偏りのあるデータです。
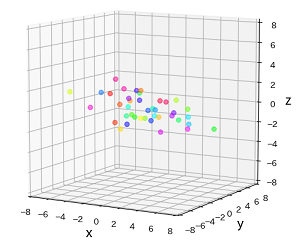
この場合も、PCAでは広く散らばっている方向である2つの軸(平面)を求めます。さらに各点からこの平面に垂線を下して射影することで、2次元平面上のデータとして捉えることができます。各点から平面への射影の際にはズレ(距離)が生じますが、このズレが最小になるような平面が選ばれます。



実際にPCAを行い、同じデータを2次元に削減してプロットしたものがこちらです。上図と同じです。

ここでは可視化するために2次元→1次元や3次元→2次元の例を見ましたが、数千、数百次元から落とす場合であっても、分散が最大になる軸を見つけていき、その空間上でデータを表現することで次元を削減するという理屈は同じです。
画像データでPCAを行う
今度はsklearnの顔画像データとライブラリを用いて実際にPCAを行ってみます。
用いるデータセットは次のような、400枚の顔画像のデータセットです。1人につき10枚(=40人分)ありますが、照明の当たり方や表情、顔の角度や眼鏡をかけていたりなど、どれも微妙に異なっています。また、1つの画像は64×64ピクセルで構成、つまり4096次元の特徴量を持ちます。
from sklearn.datasets import fetch_olivetti_faces faces = fetch_olivetti_faces() m = faces.images.shape[0] # 画像の個数 400 h = faces.images.shape[1] # 高さ 64 w = faces.images.shape[2] # 幅 64 X = faces.images.reshape(m, h * w) # X = faces.data.shapeでも可 print(m, h, w) # 400 64 64 print('X.shape: ', X.shape) # (400, 4096)
前から100画像を表示すると以下のような感じです。

ではPCAを使って、まずは一気に2次元にしてみます。
from sklearn.decomposition import PCA pca = PCA(n_components=2) # n_componentsに維持する主成分の数を指定する pca.fit(X) # データにモデルを適合させて主成分を見つける X_2d = pca.transform(X) # 2つの主成分に対してデータを変換(次元削減)する
ちょっと見にくいですが、X_2dをラベル付きでプロットすると下図のようになりました。
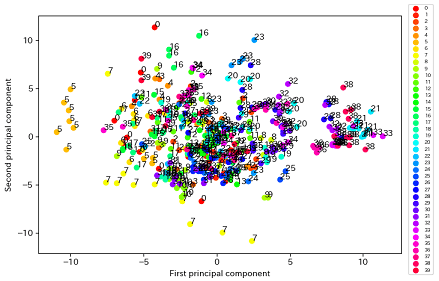
このX_2dは第1、第2主成分に元のデータを射影したものになります。
端の方では同じラベルが集まっている部分もありますが、全体的にはほぼ団子状態です。もし、この2次元まで削減したデータを用いて分類タスクなどを行おうとしても、これは無理がありそうです。ある程度予想はできましたが、4096→2次元では分類に必要な情報まで捨ててしまっていると言えます。
寄与率と累積寄与率
では、n_componentsをいくつに指定すればよいのかというと、累積寄与率をその指標とすることができます。寄与率とは主成分がどの程度元データの情報を表現しているかを表すもので、累積寄与率はその寄与率を足し合わせたものです。
コードで見てみます。
print('各主成分の寄与率: ', pca.explained_variance_ratio_) # [0.23812726 0.13993974]
この場合各主成分が保持している情報は第1主成分が約24%、第2主成分が約14%であり、合わせた累積寄与率は約38%ということになります。この2つの主成分で元データの情報の38%を表現できていることを示しています。また、寄与率は第1主成分が最も大きく、第2、第3と次第に小さくなっていきます。
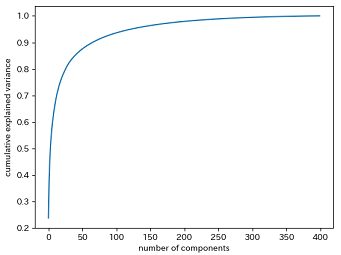
図は横軸に主成分の数、縦軸に累積寄与率をプロットしたものです。
だいたい主成分が250くらいで99%くらいですが、元データの99%の情報を保持したままでも、多くの次元を削減できることがわかります。ケースバイケースでしょうが、99%でなくとも、80~90%程度あれば充分とする場合もあるようです。その場合はより少ない主成分で保持することができます。
PCAのパラメータのn_componentsに0~1の小数を与えると、与えた割合以上の情報を保持できるだけの主成分になるよう指定することができます。
pca = PCA(n_components=0.99) pca.fit(X) print('保たれている情報: ', np.sum(pca.explained_variance_ratio_)) # 0.9900053 print('主成分の数: ', pca.n_components_) # 260
主成分の可視化
主成分はfit()後、components_属性に格納されています。その形状は以下の通りです。行は情報量が多い順にソートされており(第1主成分が先頭)、列は元データの次元数と同じになっています。
print('得られた主成分の形状: ', pca.components_.shape) # (260, 4096)
では得られた260個の主成分のうち最初の20個を表示してみます。

それぞれの画像の意味を解釈することは難しいですが、顔と背景のコントラストや、目や口、顔の上半分が明るくなっていたりなど、様々な明暗のパターンがあります。顔の輪郭やパーツなどが捉えられているのかもしれません。
顔画像に限らず、この主成分の解釈というのは簡単ではない場合が多いようです。ある程度は、主成分の符号や大きさをみることで特徴量との関係をつかみ、主成分が何を表しているかを推測することができますが、次元数が多い場合には特に難しいことかと思います。
次元の削減と復元
得られた主成分を使って、データセットの次元を削減することができます。
X_projected = pca.transform(X) print('変換後のデータの形状: ', X_projected.shape) # (400, 260)
上でも一度使いましたが、このtransformメソッドにより、データを主成分に射影することができます。この場合は、元データの99%の情報(=分散)を保ったまま、データを4096次元から260次元に削減したことになります。学習アルゴリズムに使用する場合は、このtransformされた、サイズが小さくなったデータセットを使うことで、より高速に訓練することができます。
今度は削減したデータを主成分を用いて元の次元に戻してみます。
inverse_transformメソッドに削減されたデータを与えます。
X_recovered = pca.inverse_transform(X_projected)

次元が大きく削減されていても99%の情報を保持した状態からでは、見た目ではわからないほどほぼ完全に元に近い状態に戻ります。
では、次に第10主成分(累積寄与率は82%)までで削減したデータを復元します。

データは元の特徴量空間に戻りますが、削減された情報はそのまま、つまり主成分の情報のみで復元されるので、完全には元に戻りません。少しぼかされたような感じです。
最後は、第4主成分(累積寄与率は51%)までです。

第4主成分までで次元削減したデータを復元しても、個々の区別はつかないような状態で、どれも同じような顔に見えます。
ちょっと踏み込んでPCAの意味を理解する
PCAがやっていることはデータの特徴量xから新しい変数zへのマッピング(関連付け)を定義している、といえます。そのマッピングとは、次のように特徴量xの線形結合で表され、PCAとは各xを乗算する係数wを求める手法だと解釈できます。
この変換後の新しい変数zは以下の条件のもとで求めていきます。
・できるだけ分散が大きくなるようにする*2
・互いに持つ情報に重複がない(=相関がない)
このzのことを主成分といい、分散が大きい順にとすれば、第1, 第2, …, 第k主成分となります。また、係数wは主成分の方向(軸)を表し、データi番目の特徴量
を代入して得られるzの値は、その主成分方向におけるデータiの取る値を表します。
実際に求めるには固有方程式を解くことになりますが、ここではその詳細は割愛します。しかし、PCAを勉強していると、「固有値」や「固有ベクトル」などの数学的な概念がでてきます。これらと今まで使ってきたsklearn PCAでの属性(やメソッド)との対応を少し整理して、"射影"や"復元"が実際に何をしているのかも見ていこうと思います。
print('寄与率(%): ', pca.explained_variance_ratio_) print('累積寄与率(%): ', np.cumsum(pca.explained_variance_ratio_)) print('固有値(主成分の分散): ', pca.explained_variance_) print('固有ベクトル(主成分の方向): ', pca.components_) print('主成分スコア(データの主成分方向での値): ', pca.transform(X))
固有ベクトルは主成分の数×特徴量nの行列として得られ、各行が第k主成分の係数に相当します。
また、+-の符号が反転していても、軸を表すものなので問題ありません。この固有ベクトルは長さが1の単位ベクトルであり、互いにすべて直交(=内積を取ると0)しています。
また、寄与率は以下のように固有値すべての和が1になるように変換したもののことです。
print('explained_variance_ratio_: ', pca.explained_variance_ / np.sum(pca.explained_variance_))
transformメソッドで得られるのは主成分軸での値(主成分スコア)で、次の2つのコードは同じことをしています。このとき用いる主成分を元の特徴量の次元より少なくすることで次元削減ができるのでした。
X_projected1 = pca.transform(X) X_projected2 = np.dot((X - np.mean(X, axis=0)), pca.components_.T) # 平均はpca.mean_でも可
pca.componentsは行ベクトルなので、転置して内積を取ります。また、新しい座標軸の中心を0にするため、(各列の)平均を引いた値を使います。データを最初に標準化しておき平均が0になっていれば引く必要はありません。
次は元の特徴空間に戻すinverse_transform()メソッドです。
これは一度変換したものを元に戻すプロセスです。transformするときに使った行列(つまり、pca.components_.T)の転置行列を用いますが、主成分の数によって復元度が異なります。PCAのパラメータのn_componentsに何も与えなければ*3、pca.components_はn×nの直交行列で得られ、これは転置をとれば逆行列になるので完全に元に戻すことができます。次のコードで表せます。
X_recovered1 = pca.inverse_transform(X_projected1) X_recovered2 = np.dot(X_projected2, pca.components_) + np.mean(X, axis=0) # 平均はpca.mean_でも可
・主成分負荷量
データの各特徴量と主成分スコアの相関係数で-1~1の値をとります。データの単位や桁が違わなければ固有ベクトルをそのまま見てもある程度のことがわかるが、そうでない場合は主成分負荷量を求める。これを見れば、主成分の解釈がしやすい場合があるとのこと。
固有ベクトルに固有値の正の平方根をかけて求めます。
# 主成分負荷量 loading = pca.components_ * np.sqrt(pca.explained_variance_) loading = loading / np.std(X, axis=0, ddof=1) # 事前に標準化していなければ必要 print('主成分負荷量: ', loading)
標準化と白色化
標準化
まず、データの標準化という場合、一般にはデータの平均を引き標準偏差で割ることを指すことが多いようです。コードでは次のような操作になります。
# (データ数×特徴量)のデータ行列Xに対して X = (X - np.mean(X, axis=0)) / np.std(X, axis=0)
これは、ライブラリのStandardScalerを使った場合の以下と同じことを意味します。
from sklearn.preprocessing import StandardScaler std = StandardScaler() X_ = std.fit_transform(X)
このような操作を行う理由としては、単位が異なるなどして桁が大きく異なるような特徴量を持つデータ(例えば、身長、体重、年収などが混ざってる)の場合は、桁が大きい方の影響が強く出てしまうため、だいたい同じ範囲になるようにスケーリングすることがあります。
ただし、スケーリングする場合は(最大値 - 最小値)などで割ることもあるなど、それほど厳密に規定されたものではなく、特徴量間のスケールがだいたい合えば良い、ということのようです。
私がcourseraの機械学習講座を受けたときはデータ前処理そのものについては「PCA適用前に必須」という表現だったかと思いますが、①平均を引く、②1の後、スケーリングもすることがある、と話されていたように思います。
平均を引くことで、射影した際に主成分軸での原点は0になります。sklearnの場合は主成分軸への射影の際には、内部的にきちんと平均を引いた上で処理されています。平均を引くだけでは、得られる固有ベクトルや固有値に差はありません。
ということで、各操作は使うライブラリやデータによっても必要性は変わってくると言えそうです。以下のリンク先ではより詳しく書かれています。
主成分分析で標準偏差で割るべき?に対する議論 #Python - Qiita
白色化
sklearnのPCAにはwhitenというオプションがあり、デフォルトではFalseですが、これをTrueにすると、transformで変換した後のデータの分散が1になるように調整します。これにより、単位や平均が異なる特徴量でも同じスケールで比較できるようになり、問題によっては性能が上がることもあるそうです。
sklearnのソースをみればわかりますが、平均が0になるように変換したX_transformedに対して標準偏差で割っています。
# sklearnのソース if self.whiten: X_transformed /= np.sqrt(self.explained_variance_)
意味的には変換したデータにStandardScalerをかけるのと同じですが、こちらは母集団の標準偏差となっているのでそのまま使うと微妙に値に違いが出ます。標本標準偏差(不偏分散による標準偏差)で割るとsklearnと同じになります。
# 白色化 X_projected2 = np.dot((X - np.mean(X, axis=0)), pca.components_.T) # ddofオプションで指定してやるとn-ddofで割る X_projected2 /= np.std(X_projected2, axis=0, ddof=1)
参考
・Coursera Machine Learning: Dimensionality Reduction
・主成分分析(馬場康維) 1(全3回)改訂版
・15stepで踏破 自然言語処理アプリケーション開発入門
今回のコードです。
import math import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import fetch_olivetti_faces from sklearn.decomposition import PCA from sklearn.datasets import fetch_lfw_people from sklearn.preprocessing import StandardScaler # 顔画像データを主成分分析する # 複数の顔画像を1枚のパネルで表示する. 与える画像の個数によってはうまく表示されないことがあるので注意. # x: (画像の個数×次元数), w: 幅, h: 高さ def display_data(x, h, w): m, n = x.shape rows = math.floor(np.sqrt(m)) cols = math.ceil(m / rows) pad = 1 # 画像間の余白 # (縦に並べる枚数分のピクセル)×(横に並べる枚数分のピクセル)の配列を用意. ここに1画像毎の値を詰め込んでいく disp_array = np.zeros((pad + rows * (h + pad), pad + cols * (w + pad))) curr_ex = 0 for j in range(1, rows + 1): for i in range(1, cols + 1): max_val = max(abs(x[curr_ex, :])) # 各画像の明度差をなくすため最大値で割る h_pos = pad + (j - 1) * (h + pad) + np.array([i for i in range(0, h + 1)]) w_pos = pad + (i - 1) * (w + pad) + np.array([i for i in range(0, w + 1)]) disp_array[h_pos[0]:h_pos[-1], w_pos[0]:w_pos[-1]] = \ x[curr_ex, :].reshape(h, w) / max_val curr_ex += 1 fig, ax = plt.subplots(figsize=(6, 6)) ax.imshow(disp_array, cmap='gray') ax.axis("off") plt.show() if __name__ == '__main__': # データセット(顔画像)の読み込み faces = fetch_olivetti_faces() # 別の顔画像のデータセット. こちらでもそのまま使える # faces = fetch_lfw_people(min_faces_per_person=20, resize=0.7) m = faces.images.shape[0] # 画像の個数 40 h = faces.images.shape[1] # 高さ 64 w = faces.images.shape[2] # 幅 64 X = faces.images.reshape(m, h * w) print(m, h, w) print('X.shape: ', X.shape) # 400 x 4096 x.shapeはfaces.data.shapeでも可 display_data(X[:100, ], h, w) # PCA適用前に標準化(平均0, 分散1にする)を行う sc = StandardScaler() X = sc.fit_transform(X) # PCAオブジェクトを生成. n_componentsに保持する主成分の数を指定する pca = PCA(n_components=2) # データにモデルを適合させて主成分を見つける pca.fit(X) # 最初の2つの主成分に対してデータを変換(次元削減)する X_2d = pca.transform(X) # 主成分によってどの程度カバー出来ているかの割合 print('各主成分の寄与率: ', pca.explained_variance_ratio_) # 第1主成分と第2主成分でプロット. cmap = plt.get_cmap("hsv") for i, label in enumerate(faces.target): plt.scatter(X_2d[i, 0], X_2d[i, 1], color=cmap(label / len(faces.target) * 10)) plt.text(X_2d[i, 0], X_2d[i, 1], label) # プロットした点にラベルをつける plt.xlabel("First principal component") plt.ylabel("Second principal component") for i in set(faces.target): plt.scatter([], [], color=cmap(i / len(faces.target) * 10), label=i) plt.legend(bbox_to_anchor=(1.02, 1.05), loc='upper left', borderaxespad=0, fontsize=6) plt.show() # 累積寄与率のプロット pca = PCA() pca.fit(X) plt.plot(np.cumsum(pca.explained_variance_ratio_)) # 累積和を取得して表示 plt.xlabel('number of components') plt.ylabel('cumulative explained variance') plt.show() pca = PCA(n_components=0.99) # 4, 10など変えてみる pca.fit(X) print('保持されている情報(%): ', np.sum(pca.explained_variance_ratio_)) # 0.9900053 print('主成分の数: ', pca.n_components_) # 260 print('得られた主成分の形状: ', pca.components_.shape) # (260, 4096) # 最初の20主成分のみを表示 display_data(pca.components_[:20, ], h, w) # データを主成分に射影して次元を削減する X_projected = pca.transform(X) print('削減後のデータの形状: ', X_projected.shape) # (400, 260) # 主成分で維持された情報を復元 X_recovered = pca.inverse_transform(X_projected) print('復元後のデータの形状: ', X_recovered.shape) # (400, 4096) # 表示前に標準化前の状態に戻す X_recovered = sc.inverse_transform(X_recovered) display_data(X_recovered[np.arange(0, 80, 10),], h, w) # 前から8人を表示
import numpy as np import matplotlib.pyplot as plt from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler if __name__ == '__main__': # 顔画像では次元が大きすぎるので小さめのデータセットを用いる. # 得点データを想定. 国, 社, 数, 理, 英 X = np.array([ # 平均 総合得点 [68, 62, 55, 67, 48], # 60 300 [46, 29, 38, 35, 31], # 35.8 179 [87, 48, 66, 65, 56], # 64.4 322 [33, 26, 35, 46, 24], # 32.8 164 [51, 46, 51, 56, 51], # 51 255 [50, 33, 45, 49, 38], # 43 215 [74, 61, 65, 93, 58], # 72 351 [84, 63, 79, 82, 100], # 81.6 408 [72, 54, 45, 59, 40], # 54 270 [41, 28, 54, 43, 29]], # 39 195 dtype=float) # 標準化 std = StandardScaler() X = std.fit_transform(X) pca = PCA(whiten=True) # whiten=True pca.fit(X) print('X.shape: ', X.shape) print('寄与率(%): ', pca.explained_variance_ratio_) print('寄与率(%)と同じ: ', pca.explained_variance_ / np.sum(pca.explained_variance_)) print('累積寄与率(%): ', np.cumsum(pca.explained_variance_ratio_)) print('固有ベクトル: ', pca.components_) print('固有ベクトルの形状: ', pca.components_.shape) print('固有値: ', pca.explained_variance_) print('主成分スコア: ', pca.transform(X)[0, :]) # 主成分負荷量(主成分と元の変数の相関係数) loading = pca.components_ * np.sqrt(pca.explained_variance_) loading = loading / np.std(X, axis=0) print('主成分負荷量: ', loading) # また各主成分は互いにすべて直交しているため、自分以外のベクトルとの内積は0となる for i in range(0, len(pca.components_)): for j in range(0, len(pca.components_)): print(str(i) +'・' + str(j) + ' :', np.dot(pca.components_[i], pca.components_[j])) # 主成分スコア(主成分軸の空間にデータを射影させたときの値) # 固有ベクトルpca.components_とxの内積は主成分軸における成分を表す # whiten=Falseのときは以下の2つは同じ X_projected1 = pca.transform(X) X_projected2 = np.dot((X - np.mean(X, axis=0)), pca.components_.T) print('X_projected1: ', X_projected1[0, :]) print('X_projected2: ', X_projected2[0, :]) # whiten=Trueの場合は以下と同じ pca_w = PCA() X2 = X - np.mean(X, axis=0) pca_w.fit(X2) X_projected3 = np.dot(X2, pca_w.components_.T) X_projected3 /= np.std(X_projected3, axis=0, ddof=1) # ddofオプションで指定してやるとn-ddofで割る print('X_projected3: ', X_projected3[0, :]) # 主成分スコアの表示 for i in range(0, len(X)): plt.scatter(X_projected1[i, 0], X_projected1[i, 1]) plt.text(X_projected1[i, 0], X_projected1[i, 1], str(i+1)) plt.axvline(x=0) plt.axhline(y=0) plt.xlabel('主成分1') # 総合点 plt.ylabel('主成分2') # ??? plt.show() # 復元. 以下の2つは同じ X_recovered1 = pca.inverse_transform(X_projected1) X_recovered2 = np.dot(X_projected2, pca.components_) + np.mean(X, axis=0) print(X_recovered1[0, :]) print(X_recovered2[0, :])
