ロジスティック回帰による多クラス分類 - 薬剤師のプログラミング学習日記

前回は2値分類でしたが、今回はロジスティック回帰モデルにおける多クラス分類のコードを書きます*1。今までの流れだと、モデルの表現と目的関数、その偏微分がわかれば勾配降下法でモデルのパラメータを求め分類器を作ることができたので、それを目指します。

ロジスティック回帰の多クラス分類モデル
目的関数と偏微分
正解ラベルのone-hot表現
実装してデータを分類してみる
- irisデータの概要
文書を分類してみる
参考

ロジスティック回帰の多クラス分類モデル

n個の特徴量 $x_1, x_2, \ldots, x_n$ を用いて、 $c$ 個のクラス数に分類される場合のモデルを以下のように考えます。

$\small{ X = \left( \begin{array}{cccc} x_{0}, x_{1}, \ldots, x_{n} \end{array} \right) , ~~ \Theta = \left( \begin{array}{cccc} \theta_{00} & \theta_{01} & \ldots & \theta_{0(c-1)} \\ \theta_{10} & \theta_{11} & \ldots & \theta_{1(c-1)} \\ \vdots & \vdots & \ddots & \vdots \\ \theta_{n0} & \theta_{n1} & \ldots & \theta_{n(c-1)} \end{array} \right) , ~~ Z = \left( \begin{array}{cccc} z_{0}, z_{1}, \ldots, z_{c-1} \end{array} \right) }\\$

$X$ は特徴量：1×(n+1)の行列。 $x_0$ を追加している。
$\Theta$ はモデルのパラメータ：(n+1)×cの行列
$Z$ は行列Xとθの積 $X\Theta$ ：1×cの行列

特徴量の行列(ベクトル)Xには $x_0=1$ と定義した $x_0$ を追加するので、特徴量の数は(n+1)となります。また、添え字は後に書くコードに合わせて0からとしました。
この $Z$ は2値分類モデルの $\theta^Tx$ に当たります。 $w_k^Tx+b_k$ と表記されているものもありますが、 $X$ に $x_0$ を追加することで同じになると考えて良いと思います。

2値分類のときは $\theta^Tx$ をシグモイド関数に通すことで出力が0～1になり、その値を一方のクラスに属する確率としてみることで分類しました。
多クラス分類では、行列Xとθの積Zを各クラスに属する確率を出力することができる以下のソフトマックス関数*2に通します。

$\rm{\displaystyle{y_k = \frac{ \exp( z_k)}{\displaystyle{\sum_{i=1}^{c} \exp( z_i)}}}}$

クラス数が全部で $c$ のときの $k$ 番目の出力 $y_k$ を表します。
$\sum$ の添え字 $i$ は上の表記に合わせると0からc-1ですが、要するにクラス数全部の合計です。
このソフトマックス関数の出力 $y_k$ は0～1となり、その総和は1となります。
例えば、クラス数が3の分類を行う場合に行列の積 $X\Theta$ の結果[-2.2, 0.3, -1.1]をソフトマックス関数の入力とした場合、出力は[0.06, 0.75, 0.19]のようになります。これは「1番目のクラスである確率が6%、2番目は75%, 3番目は19%」というように解釈します。

目的関数と偏微分

最小化したい目的関数Eは次の数式で表されます。

$\rm{\displaystyle{E = -\sum_{k}t_k \ log(y_k)}}$

この式がしていることは1つのデータについて、正解ラベルに対応する部分の出力(予測)の自然対数を計算しラベルの値と掛け算した後、クラスのインデックスkについて全ての和を取っています。例で言うと、ソフトマックス関数の出力 $y$ が[0.06, 0.75, 0.19]、正解ラベル $t$ が[0, 1, 0]だったとすると、

-log(0.06)×0-log(0.75)×1-log(0.19)×0= 0.287..

となります。正解ラベルが0の部分の出力は掛け算しても結局0となるので、正解ラベルが1に対応するところだけの出力の-logを求めているということです。この値は、正解ラベルのところの出力の確率の数値が大きい程、小さくなります。
また、ここではより広い意味で使われる(損失関数を含む)目的関数という言葉を使っていますが、上の関数は交差エントロピー誤差(cross entropy error)と呼ぶそうです。
訓練データ全てについての和を求めると、次のようになります。

$\rm{\displaystyle{E = -\sum_{m}\sum_{k}t_{mk}log(y_{mk})}}$

先に示した式で、データ数ｍについて全ての項の和を取っただけです。
ここで、参考文献2ではこの式を訓練データ数で割ることによってデータ1個あたりの平均の値を求めていましたが、これは全てのデータを対象にして和を求めるのは少々時間がかかってしまうからだそうです。今回、分類しようとしているデータは大した数ではありません*3ので、今回は平均ではなく勾配降下法のたびに全データの和を求めようと思います。

次は、偏微分です。
コードに落とし込む上で必要になる行列の形式で書くと次のようになります。

$\displaystyle{ \frac{\partial E}{\partial \Theta} = - X^T (T - Y)}$

$\displaystyle{ \frac{\partial E}{\partial \Theta}}$ ：勾配(特徴量の数×クラス数) $\Theta$ と同じ形状をしている
$X^T$ ：特徴量の転置行列(特徴量の数×データ数)
$T$ ：正解ラベル(データ数×クラス数)
$Y$ ：ソフトマックス関数の出力(データ数×クラス数)

モデルのパラメータ $\Theta$ の更新は今までと同じ最急降下法を使って以下の式で行います。

$\Theta := \displaystyle{ \Theta - \alpha\frac{\partial E}{\partial \Theta}}$

正解ラベルのone-hot表現

one-hot表現とは、特定の要素だけが1で、それ以外は0となっている表現、又はベクトルのことです。正解ラベルにおいては、例えば、クラス数が3、正解ラベルが[2](0から始まるとする)だとすると、one-hot表現では[0, 0, 1]、正解ラベルが[0]なら[1, 0, 0]のようになります。
今回のプログラムではone-hot表現での正解ラベルが必要になるので、この形式でない場合は変換してやります。

実装してデータを分類してみる

sklearnのデータセットにあるアイリス（ヤマメ）のデータを分類してみます。

irisデータの概要

from sklearn.datasets import load_iris
 
iris = load_iris()
print('データの形状: ', iris.data.shape)  # 　(150, 4) データ数×特徴量
print('花の種類: ', iris.target_names)   # ['setosa' 'versicolor' 'virginica']
print(iris.data[:5,])     # データの前から5個を表示
# [[5.1 3.5 1.4 0.2]
#  [4.9 3.  1.4 0.2]
#  [4.7 3.2 1.3 0.2]
#  [4.6 3.1 1.5 0.2]
#  [5.  3.6 1.4 0.2]]
print(iris.target)        # ラベル
# [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#  0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#  1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
#  2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#  2 2]

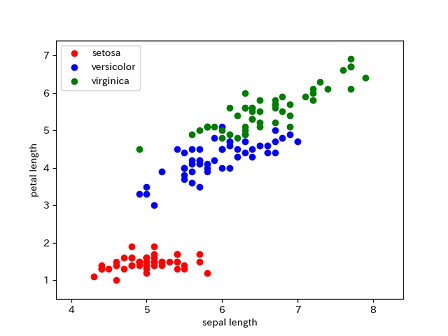
データ数は全部で150、特徴量は4つあり、その各数字は[ガクの長さ、幅、花弁の長さ、幅]を表しています。また、ラベルを見ると前から50個ずつ0, 1, 2の3種類が割り当てられていることがわかります。ということでクラス数は3です。
今回はデータをプロットしたいので、4つの特徴量のうちガクの長さ(sepal length)と花弁の長さ(petal length)の2つを使用して分類を試みます。
f:id:enokisaute:20200625192903p:plain

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
 
# 多クラスロジスティック回帰でirisのデータを分類
 
def softmax(z):
    if z.ndim == 2:
        m, n = z.shape
        # 大きすぎる値だとexp(x)はオーバーフローするため, 各データごとの最大値で引いておく.
        # 大小関係は変わらず結果は同じ.
        z = z - np.max(z, axis=1).reshape(m, -1)
        return np.exp(z) / np.sum(np.exp(z), axis=1).reshape(m, -1)
    else:
        return np.exp(z) / np.sum(np.exp(z))
 
def to_onehot(label):
    # データ数×クラス数のゼロ行列をつくる
    T = np.zeros((label.size, len(set(label))))
    for idx, row in enumerate(T):
        row[label[idx]] = 1     # ラベルの番号のインデックスのみ1として格納
    return T
 
# y:予測, t:正解ラベル
def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))   # np.log(0)を防ぐため+delta
 
def compute_loss(theta, x, t):
    h = softmax(np.dot(x, theta))
    error = cross_entropy_error(h, t)
    diff = (t - h)
    grad = -np.dot(x.T, diff)
    return error, grad
 
def gradient_descent(x, y, theta, alpha, num_iters):
    loss_history = np.zeros(num_iters)
    for i in range(0, num_iters):
        loss_history[i], grad = compute_loss(theta, x, y)
        theta = theta - alpha * grad
    return loss_history, theta
 
 
if __name__ == '__main__':
    iris = load_iris()
    X = iris.data[:, [0, 2]]  # 全てのデータの0, 2列目(ガクの長さ, 花弁の長さ)を抽出
 
    # データの可視化
    plt.scatter(X[:50, 0], X[:50, 1], color='r', label='setosa')  # 0~49
    plt.scatter(X[50:100, 0], X[50:100, 1], color='b', label='versicolor')  # 50~99
    plt.scatter(X[100:150, 0], X[100:150, 1], color='g', label='virginica')  # 100~149
    plt.xlabel('sepal length')
    plt.ylabel('petal length')
    # 軸の範囲を設定
    x1_min, x1_max = min(X[:, 0]) - 0.5, max(X[:, 0]) + 0.5
    x2_min, x2_max = min(X[:, 1]) - 0.5, max(X[:, 1]) + 0.5
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    # plt.show()
 
    m, n = X.shape  # m:訓練データ数, n:特徴量の数 (150, 2)
    c = len(set(iris.target))   # クラスの数
    intercept_term = np.ones((m, 1))
    X = np.hstack((intercept_term, X.reshape(m, -1)))   # x0=1の項をXに追加. Xはデータ数×(n+1)になる
    initial_theta = np.zeros((n + 1, c))    # (n+1)×クラス数
    target = to_onehot(iris.target)     # 正解ラベルをone hotに変換
 
    alpha = 0.0001      # 学習率
    num_iters = 20000
    loss, theta = gradient_descent(X, target, initial_theta, alpha, num_iters)
 
    # 訓練データにおける正解率
    predict = softmax(np.dot(X, theta))
    pred_class = predict.argmax(axis=1)     # 分類器の予測したクラス
    print("Train Accuracy: ", np.mean(iris.target == pred_class))
 
    # 決定境界の描画
    x_1 = np.linspace(x1_min, x1_max, 200)
    x_2 = np.linspace(x2_min, x2_max, 200)
    x1, x2 = np.meshgrid(x_1, x_2)
    # 格子点に対して分類器が予測を行う. thetaの0行目は切片項なので, 1, 2行目を掛けた後で切片項をプラスする
    pred = softmax(np.dot(np.array([x1.ravel(), x2.ravel()]).T, theta[1:3, :]) + theta[0, :])
    z = pred.max(axis=1)    # pred.shapeは40000×3. 各行ごとの最大値を選ぶ
    z = z.reshape(x1.shape)
    # 等高線で描画する
    plt.contour(x1, x2, z, 10, alpha=0.6, linewidths=0.5)
    plt.legend()
 
    # lossの履歴をプロット
    plt.figure(2)
    plt.plot(loss)
    plt.xlabel("iteration")
    plt.ylabel("loss")
    plt.show()

Xの0列目に $x_0$ =1の項を追加して、 $\Theta$ を0で初期化、正解ラベルをone-hot表現に変換した後で、最急降下法を使って $\Theta$ を更新していきます。
交差エントロピー誤差関数ではyとtのnumpy配列同士で、ラベルに対応する要素同士の積を行っています。
ソフトマックス関数は入力が2次元配列の場合、分母のzをデータ毎に合計した後、データ数×1の形にreshapeすることで対応する分子のnp.exp(z)に除算を行っています。
この部分のコードは参考文献2のものを参考にさせていただきました。

訓練データにおける正解率は次のようになりました。

Train Accuracy:  0.9466666666666667

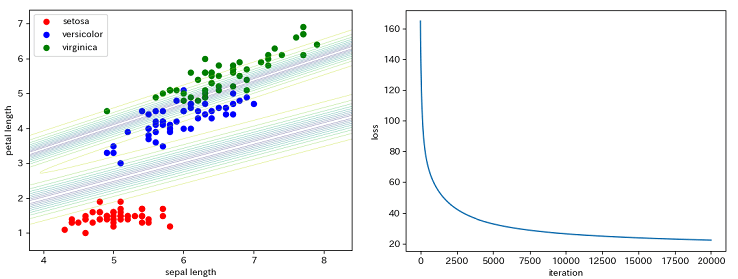
決定境界の描画(下左図)では、直線を引く方法がどうもよくわからなかったので、格子点を作成しその各点について分類器に予測を行わせることで等高線を描画しました。
右図はイテレーション毎のlossの推移です。
f:id:enokisaute:20200622193536p:plain

文書を分類してみる

線形モデルであるロジスティック回帰はテキストデータのような疎なデータに対してもうまく機能するとのことで、今度は文書データで分類を試みます。
対象となるデータセットは以前「Bag of WordsをPythonで書いてみる」でも使用したsklearnの20のニュースグループのデータセットです。
このデータセットは20のトピックで構成されたテキストデータで、データ数は全部で約18000あります。
詳しくはこちらをご参照ください。
7. Dataset loading utilities — scikit-learn 0.23.2 documentation

import re
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction import stop_words
from sklearn.model_selection import train_test_split
 
# 多クラスロジスティック回帰で文書データを分類
 
def softmax(z):
    if z.ndim == 2:
        m, n = z.shape
        # 大きすぎる値だとexp(x)はオーバーフローするため, 各データごとの最大値で引いておく.
        # 大小関係は変わらず結果は同じ.
        z = z - np.max(z, axis=1).reshape(m, -1)
        return np.exp(z) / np.sum(np.exp(z), axis=1).reshape(m, -1)
    else:
        return np.exp(z) / np.sum(np.exp(z))
 
def to_onehot(label):
    # データ数×クラス数のゼロ行列をつくる
    T = np.zeros((label.size, len(set(label))))
    for idx, row in enumerate(T):
        row[label[idx]] = 1     # ラベルの番号のインデックスのみ1として格納
    return T
 
# y:予測, t:正解ラベル
def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))   # np.log(0)を防ぐため+delta
 
def compute_loss(theta, x, t):
    h = softmax(np.dot(x, theta))
    error = cross_entropy_error(h, t)
    diff = (t - h)
    grad = -np.dot(x.T, diff)
    return error, grad
 
def gradient_descent(x, y, theta, alpha, num_iters):
    loss_history = np.zeros(num_iters)
    for i in range(0, num_iters):
        loss_history[i], grad = compute_loss(theta, x, y)
        theta = theta - alpha * grad
    return loss_history, theta
 
 
if __name__ == '__main__':
    reg = re.compile(r"[<>|:-]")
 
    # テスト用の単純なtokenizer. 一部記号を削除してスペースで区切るだけ.
    def tokenizer(text):
        text = reg.sub('', text)
        return text.split()
 
    # skearnのストップワードを取得
    sw = stop_words.ENGLISH_STOP_WORDS
    # データセットの読み込み.
    newsgroups = fetch_20newsgroups(subset='train')
    # BoWを求める
    vectorizer = CountVectorizer(tokenizer=tokenizer,
                                 min_df=0.003,
                                 stop_words=sw)
    # データ, ラベルとも前から5000のみ切り出す
    ng_data = newsgroups.data[:5000]
    ng_target = newsgroups.target[:5000]
    # toarray()で疎行列からnumpy配列に変換しておく
    bow = vectorizer.fit_transform(ng_data).toarray()
    print('bow.shape :', bow.shape)    # (5000, 6147)
 
    m, n = bow.shape    # m:訓練データ数, n:特徴量の数
    intercept_term = np.ones((m, 1))
    x_feature = np.hstack((intercept_term, bow.reshape(m, -1)))
 
    # データをtrain:test = 7:3に分割
    X_train, X_test, y_train, y_test = train_test_split(x_feature, ng_target, test_size=0.3,
                                                        random_state=1)
 
    c = len(set(ng_target))  # クラスの数
    initial_theta = np.zeros((n + 1, c))  # (n+1)×クラス数
    onehot_y_train = to_onehot(y_train)  # 正解ラベルをone hotに変換
    alpha = 0.0001      # 学習率
    num_iters = 1000
    loss, theta = gradient_descent(X_train, onehot_y_train, initial_theta, alpha, num_iters)
 
    # 訓練データの正解率
    predict = softmax(np.dot(X_train, theta))
    pred_class = predict.argmax(axis=1)     # 分類器の予測したクラス
    print("Train Accuracy: ", np.mean(y_train == pred_class))
 
    # テストデータの正解率
    predict = softmax(np.dot(X_test, theta))
    pred_class = predict.argmax(axis=1)
    print("Test Accuracy: ", np.mean(y_test == pred_class))
 
    # sklearnのロジスティック回帰によるテストデータの正解率
    model = LogisticRegression()
    model.fit(X_train, y_train)
    print("Test Accuracy(sklearn): ", model.score(X_test, y_test))
 
    # lossの履歴をプロット
    plt.figure(2)
    plt.plot(loss)
    plt.xlabel("iteration")
    plt.ylabel("loss")
    plt.show()

今回は作成したロジスティック回帰による分類器がうまく動くかを確かめるのが目的なので、使用するデータはsubset='train'で読み込んだ5000のみとして、これを訓練データ70%, テストデータ30%に分割しました*4。
前からスライスで切り出しましたが、データの並び順はクラスがランダムになるよう最初からシャッフルされているので、5000だけ使うとなると、各クラスがだいたい250ぐらいということになります。
データを少なくした理由は、上の方で少し触れましたが、交差エントロピー誤差を求めるのに時間がかかり過ぎる実装となっているためです。

データのベクトル化にはsklearnのCountVectorizerを使用してBoWを得ています。
ここで、Bowの形状をみると行列のサイズは5000×6147(データ数×語彙数)ですが、BoWを求める際にストップワード(sw)や出現頻度が低い語を除外(min_df)の設定をしなければ、語彙数は23万を超えていました。あまりにも大きな特徴量の場合はPCAなどを使って次元を削減する方法もありますが、今回はCountVectorizerのパラメータを設定することである程度小さなサイズになるようにしました。

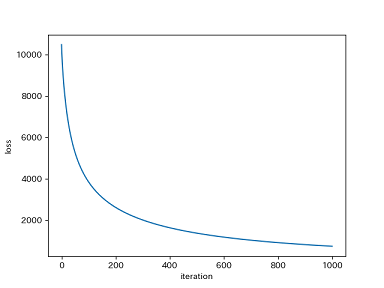
プログラムの実行結果は次のようになりました。
f:id:enokisaute:20200625005136p:plain

Train Accuracy:  0.9905714285714285
Test Accuracy:  0.7786666666666666
Test Accuracy(sklearn):  0.7613333333333333

上2つが今回作成したプログラムの結果、一番下はsklearnのロジスティック回帰によるものです。とりあえず、まともに動いているようですが、テストデータの正解率は78%とまだまだです。
訓練データの正解率は99%あり、こちらだけが高いので過学習でしょう。未知のデータに対する汎化性能が低い、という状態です。もっとデータを増やすと性能が改善すると考えられます。他にも、特徴量を増やして正則化を導入*5する、などの方法もあります。

今回はロジスティック回帰モデルを実装しました。正則化はなしでやりましたが、このあたりのアルゴリズムはまだ何をしているかが理解しやすく、コードも書きやすい気がします。

参考

・ Deep Learning Javaプログラミング深層学習の理論と実装
・ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装
・多クラス分類ロジスティック回帰 - Pythonと機械学習
・Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎