あらかじめMNISTで学習しておいたCNNモデルを自分で集めた手書き数字画像データセットに対して精度が高くなるよう再学習しました。
- 事前学習済みCNNモデルの重みを微調整する
- 手書き数字画像データセットを可視化する
- MNIST学習モデルの自作データセットにおける精度
- 自作データセットを使って再学習する
- 誤認識した数字画像を表示して確認する
- 参考
事前学習済みCNNモデルの重みを微調整する
自分の環境で出てくる実データに対する認識精度をより高めるために、似たデータであらかじめ学習しておいたモデルを利用する、ということをやってみたいと思います。
これは、ディープラーニング関連で「ファインチューニング(微調整)」という用語で説明される手法が近いようですが、私の中で少し定義が曖昧な部分があったので、ここでは「再学習」としました。*1
手書き数字画像データセットを可視化する
数字画像として見るだけではなくPCAやTSNEといった可視化手法も試して、MNISTデータセットと比較してみます。
なお、ここでの自作の数字画像データセットについては、自分で収集した手書き数字画像に前処理を施し、データ拡張などを行いデータセットとしたものです。よろしければこちらの記事をご参照ください。
www.yakupro.info
グレースケール画像でデータを描画
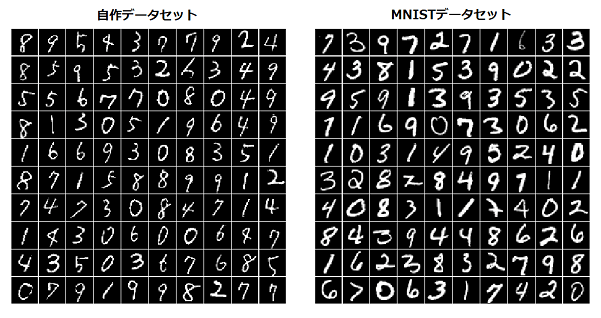
まずはグレースケール画像です。各データセットをロードしてシャッフルした後、それぞれ先頭の100画像を描画してみました。
比較するとMNISTの方は全体的に文字が太く、文字のくせもバラエティに富むというか、強い気がします。一方自作データの方は太さはどれも細く、文字のくせはおとなしめです。また、文字がかすれていたり、数字の一部が欠損しているようなものもみられます。
PCAを使って2次元の空間で見る
PCA(主成分分析)でこれらのデータを2次元にしてプロットしました。
自作データとMNISTそれぞれ10000枚で主成分分析を行い、第1, 第2主成分を用いてプロットして各点をラベルごとに色分けしています。
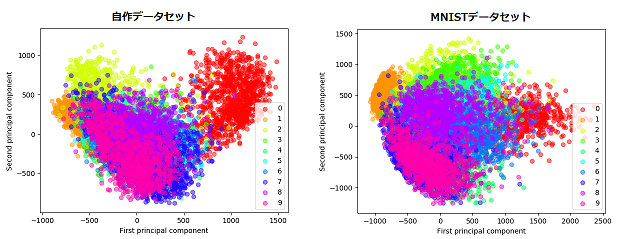
各数字のデータ点がプロットされる位置関係は似ていなくはないですが、MNISTの方が広がりがあり、データ点の重なりが少ないです。
ちなみに、各主成分の寄与率は次のようになりました。
print('各主成分の寄与率: ', pca.explained_variance_ratio_) # [0.08329232 0.05061341] 自作データセット # [0.10047663 0.07544487] MNISTデータセット
各主成分が保持する情報の割合もMNISTの方が(わずかですが)多いことがわかります。
t-SNEによる可視化
t-SNEは高次元データの可視化に用いられる手法の1つですが、元の特徴空間におけるデータ間の類似度をできる限り維持するため、類似しているデータは低次元に変換後も近くに配置される、という特徴があります。
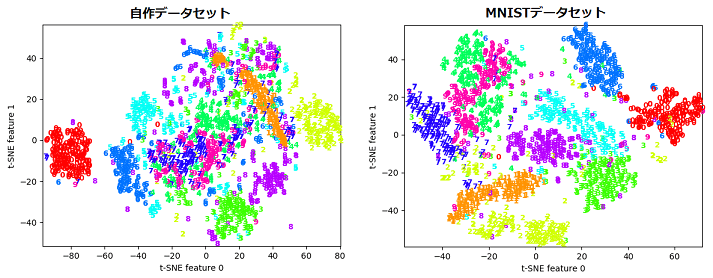
各データセット2000ずつプロットしてみました。
こちらも、各ラベルがきれいに分離されているのはMNISTの方でした。自作データセットの方は0と1と2あたりはひとつの密なクラスターにまとまっていますが、他は明確に分離されているというほどではありません。とはいえ、7と9と4など少し区別がつきにくいもの同士が近くに位置しているなど共通している部分もみられます。
違いの理由はデータの水増し?
自作データもMNISTのように作っているのに、なぜこのような違いが出るのかを疑問に思い、一度Data Augmentation(データ拡張)なしのデータだけで自作データセットを作り、同じようにPCAとt-SNEをやってみたところ下図のようになりました。


どうやらData Augmentationがデータの複雑さに影響しているというのは間違いなさそうです。しかし、そもそもData Augmentationは元データを変形等させて様々なデータを人工的に作成することにより学習モデルの頑健性を高め、精度を向上させるというものでした。なので、自作データのプロットは混沌としていましたが、より多くの様々なデータをモデルに与えるという意味ではこれでよかったのではないかと思います(逆に言うとMNISTが綺麗すぎるんだろうか)。
import math import matplotlib.pyplot as plt import numpy as np import tensorflow as tf from sklearn.decomposition import PCA from sklearn.manifold import TSNE from digit_img import DigitImage # 前記事作成した自作データセットモジュール # 自作データセットとMNIST画像をグレースケール, PCA, t-SNEで可視化する # 手書き数字画像をグレースケールで表示 # x: (画像の枚数×次元数), w: 幅, h: 高さ def display_data(x, w, h): m, n = x.shape rows = math.floor(np.sqrt(m)) cols = math.ceil(m / rows) pad = 1 # 画像間の余白 # (縦に並べる枚数分のピクセル)×(横に並べる枚数分のピクセル)の配列を用意. ここに1画像毎の値を詰め込んでいく disp_array = np.full((pad + rows * (h + pad), pad + cols * (w + pad)), 255) curr_ex = 0 for j in range(1, rows + 1): for i in range(1, cols + 1): h_pos = pad + (j - 1) * (h + pad) + np.array([i for i in range(0, h + 1)]) w_pos = pad + (i - 1) * (w + pad) + np.array([i for i in range(0, w + 1)]) disp_array[h_pos[0]:h_pos[-1], w_pos[0]:w_pos[-1]] = \ x[curr_ex, :].reshape(h, w) curr_ex += 1 fig, ax = plt.subplots(figsize=(6, 6)) ax.imshow(disp_array, cmap='gray') ax.axis("off") plt.show() # PCAによる2次元プロット def plot_pca_features(X, labels): pca = PCA(n_components=2) features = pca.fit_transform(X) print('各主成分の寄与率: ', pca.explained_variance_ratio_) x = features[:, 0] y = features[:, 1] cmap = plt.get_cmap("hsv") for i in set(labels): # ラベルiのインデックスの要素番号を抽出 c = np.where(labels == i) plt.scatter(x[c[0]], y[c[0]], color=cmap(i * 0.1), label=i, alpha=0.5) plt.legend(loc='lower right') plt.xlabel('First principal component') plt.ylabel('Second principal component') plt.show() # t-SNEによる2次元プロット def plot_tsne_features(X, labels): tsne = TSNE(n_components=2, random_state=42) features = tsne.fit_transform(X) x = features[:, 0] y = features[:, 1] cmap = plt.get_cmap("hsv") for i, label in enumerate(labels): plt.text(x[i], y[i], str(label), color=cmap(label * 0.1), fontdict={'weight': 'bold', 'size': 9}) for i in set(labels): plt.scatter([], [], color=cmap(i * 0.1), label=i) plt.xlim(x.min(), x.max() + 1) plt.ylim(y.min(), y.max() + 1) plt.xlabel('t-SNE feature 0') plt.ylabel('t-SNE feature 1') plt.show() if __name__ == '__main__': # MNISTデータセット. テスト用画像を用いる mnist = tf.keras.datasets.mnist (_, _), (x_test, y_test) = mnist.load_data() rand_idx = np.random.RandomState(seed=42).permutation(len(x_test)) x_test, y_test = x_test.reshape(10000, 784)[rand_idx], y_test[rand_idx] display_data(x_test[:100], 28, 28) # グレースケール画像 plot_pca_features(x_test, y_test) # PCA plot_tsne_features(x_test[:2000], y_test[:2000]) # t-SNE # 自作データセット digit = DigitImage() X, y = digit.load_data('digit_dataset.pkl', normalize=False, flatten=True, one_hot_label=False) print(X.shape) # (10000, 784) X, y = X[rand_idx], y[rand_idx] display_data(X[:100], 28, 28) # グレースケール画像 plot_pca_features(X, y) # PCA plot_tsne_features(X[:2000], y[:2000]) # t-SNE
MNIST学習モデルの自作データセットにおける精度
まずはMNISTの学習だけで自作データに対してどれくらいの精度が出るかをみてみます。
使用するCNNは事前に「畳み込みニューラルネットワークを自作の手書き数字画像に利用する」で学習を行っておいたものです。
import matplotlib.pyplot as plt import numpy as np import seaborn as sns from sklearn.model_selection import train_test_split from sklearn.metrics import confusion_matrix, classification_report from tensorflow.keras.models import load_model from digit_img import DigitImage # 前記事で作成した自作データセットモジュール digit = DigitImage() X, y = digit.load_data('digit_dataset.pkl', normalize=True, flatten=False, one_hot_label=True) print(X.shape) # (10000, 1, 28, 28) print(y.shape) # (10000, 10) # ロードしたデータを学習用とテスト用に分割. シャッフルもされる _, X_test, _, y_test = train_test_split(X.reshape((len(X), 28, 28, 1)), y, train_size=0.6) # モデルをロードしてテストデータでの精度を表示 model = load_model('./my_cnn.h5') score = model.evaluate(X_test, y_test, verbose=0) print("Test accuracy: ", score[1]) # 0.9610000252723694
自作データ10000枚のうちのテストデータ4000枚における精度(accuracy)は0.961という結果でした。MNISTでは0.9925だったので3%程度低い数字となりましたが、モデルにとっては未知である自作の手書き画像でもCNNはなかなかの数字を出すことができています。
クラス分類モデルの評価指標
sklearnのconfusion_matrix()関数とclassification_report()関数を用いて混同行列(Confusion matrix)をヒートマップで描画、precision, recall, f1-scoreなどの混同行列の情報をまとめたレポートを表示しています。
これらを見ることで、どのクラス(ラベル)で誤認識が多いのかなど自分のモデルの傾向を確認したり、数値的に評価することができます。
# 混同行列をヒートマップで表示 y_test = np.argmax(y_test, axis=1) # 正解ラベル.one_hotから変換 y_pred = np.argmax(model.predict(X_test), axis=1) # モデルの予測 cm = confusion_matrix(y_test, y_pred) sns.heatmap(cm, annot=True, fmt='d') # annotでセルに値を表示, fmt='d'で整数表示 plt.show()

行は0から9までの実際に予測した結果のデータの個数となっています。たとえば、「4」の行を見てみると実際に4と予測(正解)できたもののデータの数は355、間違って8と予測したデータは31あることになります。また「8」の列に注目してみると、4のほか6や9など他の数字でも誤認識で8と間違えられてるケースが比較的多いことなどが読み取れます。
次はclassification_report()関数の出力を見てみます。
# 各評価指標のレポートを表示 print(classification_report(y_test, y_pred, digits=3)) # digitsで小数点以下の桁数を指定 # precision recall f1-score support # # 0 0.997 1.000 0.999 391 # 1 0.965 0.998 0.981 412 # 2 0.955 0.973 0.964 375 # 3 0.983 0.981 0.982 424 # 4 0.947 0.908 0.927 391 # 5 0.975 1.000 0.987 422 # 6 0.989 0.892 0.938 418 # 7 0.977 0.946 0.961 404 # 8 0.857 0.977 0.913 386 # 9 0.975 0.934 0.954 377 # # accuracy 0.961 4000 # macro avg 0.962 0.961 0.961 4000 #weighted avg 0.963 0.961 0.961 4000
表中の用語は以下のような意味です。
- precision(適合率):モデルがあるクラスと予測した内で、実際にそのクラスだった割合
- recall(再現率):あるクラスのデータを対象としたとき、モデルがどれだけの数そのクラスだと予測できるかの割合
- f1-score(F1-スコア):適合率と再現率をまとめたもの。2値の調和平均*2で表され、小さい方の値の影響を強く受けます*3。そのため、F1-スコアを大きくするには両方とも大きくないといけません。
precisionとrecallは両方とも大きい方が良いですが、この2つの値はトレードオフの関係にあります。どちらをより重視するのか、とはっきり言える場合は良いのですが、そうでない場合にもF1-スコアはこれらをまとめた1つの評価指標として有用です。
これまでも使っていたaccuracy(精度)は正確な予測の数をすべてのデータの個数で割ったもの(=正解率)のこと、supportは各クラスのデータ数のこと、macro avgは各指標の全クラス平均です。
このモデルの場合でいうと、recallが低い4や6はそれらのクラス画像を実際にそうと予測することが(他と比較して)難しい、precisionの低い8はモデルが8と予測したデータの内で、実際にはそうでないケースが多かった、ということを示しています。
クラスのデータ数が偏ったデータセットの場合、精度だけをモデル評価の基準とすると、モデルの性能を見誤る場合があります。
たとえば、数字の0はうまく分類できるが、7や9はうまく分類できないようなモデルだと、データセット内の0が極端に多ければ全体の精度としては高く出てしまいます。
そのような場合でもこれらの評価指標を用いることで、モデルを合理的に比較したり評価できるということですね。
自作データセットを使って再学習する
自作データセットで再学習を行います。といっても、することは「畳み込みニューラルネットワークを自作の手書き数字画像に利用する」とほぼ同じです(コードは省略)。
自作データセットをロード後、train_test_split()で学習用とテスト用を6:4に分割して、ロードしたモデルに与えてfit()します。
基本的な設定も同じですが、今回は学習用データ数が6000(うち検証用20%)とMNISTよりも少なかったのでbatch_sizeは128→64としました。
model.fit(X_train, y_train, batch_size=64, epochs=20, validation_split=0.2, callbacks=[EarlyStopping(monitor='val_loss', patience=2, verbose=1, mode='auto')], verbose=1)
MNISTのときと同様に、過学習しないようにEarlyStopping()を使用しています。
Epoch 1/10 75/75 [==============================] - 2s 26ms/step - loss: 0.1046 - accuracy: 0.9715 - val_loss: 0.0311 - val_accuracy: 0.9908 Epoch 2/10 75/75 [==============================] - 2s 24ms/step - loss: 0.0385 - accuracy: 0.9900 - val_loss: 0.0242 - val_accuracy: 0.9892 Epoch 3/10 75/75 [==============================] - 2s 25ms/step - loss: 0.0203 - accuracy: 0.9935 - val_loss: 0.0172 - val_accuracy: 0.9925 Epoch 4/10 75/75 [==============================] - 2s 24ms/step - loss: 0.0141 - accuracy: 0.9948 - val_loss: 0.0220 - val_accuracy: 0.9925 Epoch 5/10 75/75 [==============================] - 2s 24ms/step - loss: 0.0103 - accuracy: 0.9965 - val_loss: 0.0148 - val_accuracy: 0.9958 Epoch 6/10 75/75 [==============================] - 2s 24ms/step - loss: 0.0074 - accuracy: 0.9975 - val_loss: 0.0139 - val_accuracy: 0.9958 Epoch 7/10 75/75 [==============================] - 2s 23ms/step - loss: 0.0107 - accuracy: 0.9960 - val_loss: 0.0195 - val_accuracy: 0.9942 Epoch 8/10 75/75 [==============================] - 2s 23ms/step - loss: 0.0047 - accuracy: 0.9990 - val_loss: 0.0149 - val_accuracy: 0.9950 Epoch 00008: early stopping
学習は8エポックで終了し、テストデータ4000枚での精度は以下のようになりました。
Test accuracy: 0.9977499842643738
この自作データを学習後の状態では、最初に使ったMNISTの精度はどれくらい出るんだろうと思って試してみたところ、0.9883と出ました。元の0.9925からは少し下がってしまいましたが、その差は約0.4%です。できるだけ過学習をさせずに、自作データの方でも高い精度が出るCNNとなりました。
誤認識した数字画像を表示して確認する
できたCNNの誤認識率は0.23%ですが、どのような画像に対して認識を間違えたのか、実際に表示してみてみます。

各画像の上の数字は『正解ラベルーモデルの認識結果』を示しています。認識を間違えたのも納得できる画像もありますが、1行目の左から1番目の6と3番目の9は読んでほしかったなあ、という感想です。(2行目のラベル9は無理があったかな)
同じCNNのMNISTデータセットにおける誤認識の画像例です。

MNISTは数が多いので全部は載せていませんが、こちらの方が誤認識したという納得感はありますね。人間が見ても判別が難しいものが多い気がします。
誤認識画像をラベル・予測と共に表示するコード
関数display_error_digit()は引数として画像データ、そのラベル、モデルの予測を受け取ります。ただし、ラベル、予測はone_hot表現ではなく[3, 9, 7, ...]のような画像がどの数字であるかのnumpy配列です。以下のコードでone_hot表現から変換しています。
y_test = np.argmax(y_test, axis=1) # 正解ラベル. one_hotから変換 y_pred = np.argmax(model.predict(x_test), axis=1) # 予測
関数内では正解ラベルと予測が異なるものがあれば画像データと共にラベル・予測をリストに追加していきます。
次に、最大表示枚数よりも画像が少なければ、不足の枚数分の詰め物(空の要素)をリストに追加します。最大表示枚数以上であればここでスライスしておきます。
最後にそれらのリストをループで回して表示しています。
なお、最大表示枚数max_sizeは変更可能です。
以下のコードはMNISTデータセットにおける使用例です。
import numpy as np import matplotlib.pyplot as plt import tensorflow as tf from tensorflow.keras.models import load_model # 誤認識した画像を<正解ラベル-予測>付きで表示する # 画像データ, ラベル, 予測を引数にとる # max_size: 最大表示枚数. 36, 49, 100などの平方数を指定可 def display_error_digit(X, y_test, y_pred, max_size=25): # 正解と予測が異なる画像をリストに加えていく title, png = [], [] for i, (label, pred) in enumerate(zip(y_test, y_pred)): if label != pred: title.append(str(label) + '-' + str(pred)) # 画像のタイトル. <正解ラベル-予測> png.append(X[i].reshape(784)) d = max_size - len(png) if d > 0: # max_sizeより画像枚数が少ない場合 for i in range(d): title.append('') png.append(np.ones(784)) else: title, png = title[:max_size], png[:max_size] plt.figure(figsize=(6, 6), dpi=120) # 適宜変更 plt.subplots_adjust(wspace=0.4, hspace=0.6) for idx, (t, img) in enumerate(zip(title, np.array(png))): plt.subplot(np.sqrt(max_size), np.sqrt(max_size), idx + 1, title=t) # 行数, 列数, プロット plt.imshow(img.reshape(28, 28), vmin=0, vmax=1, cmap='gray') plt.axis('off') # 座標軸は非表示 plt.show() def preprocess(data, label_data=False, num_classes=10): if label_data: # 教師ラベルをone-hotベクトルに変換する data = tf.keras.utils.to_categorical(data, num_classes) else: data = data.astype('float32') data /= 255 return data if __name__ == '__main__': # MNISTデータセットのロードと前処理 mnist = tf.keras.datasets.mnist (x_train, y_train), (x_test, y_test) = mnist.load_data() x_train, x_test = x_train.reshape((60000, 28, 28, 1)), x_test.reshape((10000, 28, 28, 1)) x_train, x_test = [preprocess(d) for d in [x_train, x_test]] y_train, y_test = [preprocess(d, label_data=True) for d in [y_train, y_test]] # モデルのロード(またはx_train, y_trainで学習を行う) model = load_model('./my_cnn.h5') score = model.evaluate(x_test, y_test, verbose=0) print("Test accuracy: ", score[1]) # 誤認識画像の表示 y_test = np.argmax(y_test, axis=1) # 正解ラベル y_pred = np.argmax(model.predict(x_test), axis=1) # 予測 display_error_digit(x_test, y_test, y_pred)

