1-コンパートメント点滴静注モデルの血中濃度推移 - 薬剤師のプログラミング学習日記

今回は0次速度の吸収過程のある1-コンパートメントモデルのグラフを描いてみます。

点滴静注時の血中濃度推移
定常状態における血中濃度
定常状態に到達するまでの時間
点滴中止後の血中濃度推移
参考

点滴静注時の血中濃度推移

「0次速度の吸収過程」というのは薬物の吸収速度が変わらない、ということを意味し、点滴静注のような投与方法がこれに該当します。
$k_0$ という一定の速度で点滴静注した場合の血中濃度の時間推移を表す式は、次のようになります。

$\displaystyle{ C = \frac{k_0}{k_e \cdot Vd}(1 - e^{-k_e \cdot t})}$

※ $k_0$ ：点滴速度、 $k_e$ ：消失速度定数、 $Vd$ ：分布容積

定常状態における血中濃度

ここで、点滴速度を $k_0$ に保ったまま充分に長い時間が経過（ｔ→∞）したとき、 $e^{-k_e・t}$ →０となり、ke、Vdは（特定の薬物、個人において）定数であるため $C$ は一定の値（ $\frac{k_0}{k_e・Vd}$ ）となります。
この状態を定常状態（steady state）といい、このときの血中濃度 $C_{ss}$ は $k_0$ に比例します。

$\displaystyle{ C_{ss} = \frac{k_0}{k_e \cdot Vd}}$

定常状態に到達するまでの時間

次に、 $C_{ss}$ に到達するまでの時間を考えてみます。

$\displaystyle{ \frac{C}{C_{ss}} = 1 - e^{-k_e・t} ≥ 0.99}$ （Cが定常状態の99%以上）

をtについて解くと、t ≥ 6.64...× $t_{1/2}$ となり、半減期の約7倍の時間が経過するとほぼ定常状態に達することがわかります。なお、ここでは $C$ が $C_{ss}$ の99%以上としましたが、この『ほぼ定常状態』をどの程度とみなすかで何倍かは変わってきます。たとえば、95%だと半減期の約4.3倍の時間で到達することになります。

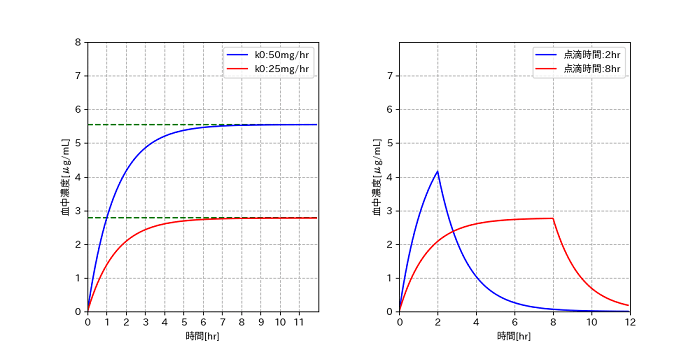
f:id:enokisaute:20200307125022p:plain
上図の左側の点滴をし続けた場合の血中濃度推移を求める部分のコードです。

import numpy as np
import matplotlib.pyplot as plt
 
k0_1 = 50   # 点滴速度(blueのグラフ)
k0_2 = 25   # 点滴速度(redのグラフ)
k = 0.693   # 消失速度定数
vd = 13     # 分布容積
 
t_half = np.log(2) / k
print("半減期: ", t_half)   # 半減期:  1.000212381760383
  
t = np.arange(0, 12, 0.1)   # 0~12時間後まで
c1 = k0_1 / (k * vd) * (1 - np.exp(-k * t))
c2 = k0_2 / (k * vd) * (1 - np.exp(-k * t))

比較のために点滴速度 $k_0$ を変えて青と赤の2つのグラフを描いています。半減期は1になるようにしています。
$k_0$ に関係なく、定常状態までの時間はだいたい半減期（1hr）の7倍となっていることがグラフからも読み取れます。

点滴中止後の血中濃度推移

点滴開始からの経過時間を $t$ 、点滴時間を $T$ とすると、 $t - T$ は点滴中止後の経過時間を表します。

$\displaystyle{ C = C_0 \cdot e^{-k_e \cdot t} = \frac{k_0}{k_e \cdot Vd}(1 - e^{-k_e \cdot T } ) \cdot e^{-k_e (t - T)}}$ 　　（t ≥ T）

点滴中止後はその時点の濃度を初濃度として1次速度で減少していきます。
これを関数として書いたものが下のコードです。
if文で点滴中と後に処理を分け、リストに計算した血中濃度を追加していきます。この関数を使って上図右側のグラフを描いています。

def calc_conc(k0, k, vd, t_in, time):
    """
    t_in: 点滴時間
    time: 経過時間. np.ndarrayで渡す
    """
    c = []
    for t in time:
        if t <= t_in:
            c.append(k0 / (k * vd) * (1 - np.exp(-k * t)))
        else:
            c.append(k0 / (k * vd) * (1 - np.exp(-k * t_in)) * np.exp(-k * (t - t_in)))
    return c

参考

徹底解説薬物動態の数学―微積分と対数、非線形

最後にコードの全文を載せておきます。

import numpy as np
import matplotlib.pyplot as plt
 
k0_1 = 50   # 点滴速度(blueのグラフ)
k0_2 = 25   # 点滴速度(redのグラフ)
k = 0.693   # 消失速度定数
vd = 13     # 分布容積
 
t_half = np.log(2) / k
print("半減期: ", t_half)
 
t = np.arange(0, 12, 0.1)   # 経過時間. 0~12時間後まで
 
c1 = k0_1 / (k * vd) * (1 - np.exp(-k * t))
c2 = k0_2 / (k * vd) * (1 - np.exp(-k * t))
 
plt.figure(figsize=(10, 5))
plt.subplots_adjust(wspace=0.35, hspace=0.35)
 
plt.subplot(1, 2, 1)    # (行数, 列数, 何番目のプロットか)
plt.plot(t, c1, color='blue', label='k0=50mg/hr')
plt.plot(t, c2, color='red', label='k0=25mg/hr')
 
# 定常状態Cssを求める
css1 = k0_1 / (k * vd)
css2 = k0_2 / (k * vd)
# Cssのところに水平ラインを引く
plt.hlines(y=css1, xmin=0, xmax=12, color='green', linestyles='dashed')
plt.hlines(y=css2, xmin=0, xmax=12, color='green', linestyles='dashed')
plt.tick_params(which='minor',width=0.5, length=5)
# 軸ラベルを表示
plt.ylabel('血中濃度[μg/mL]')
plt.xlabel('時間[hr]')
# 軸の範囲と目盛りを指定する
plt.xlim(0, 12)
plt.xticks(np.arange(0, 12, t_half))
plt.ylim(0, 8)
# グリッドの表示
plt.grid(linestyle='dashed')
# ラベルに応じた凡例を表示
plt.legend()
 
# 点滴中止後の血中濃度推移を描画
T1, T2 = 2, 8      # 点滴時間
c1, c2 = [], []
 
def calc_conc(k0, k, vd, t_in, time):
    """
    t_in: 点滴時間
    time: 経過時間. np.ndarrayで渡す
    """
    c = []
    for t in time:
        if t <= t_in:
            c.append(k0 / (k * vd) * (1 - np.exp(-k * t)))
        else:
            c.append(k0 / (k * vd) * (1 - np.exp(-k * t_in)) * np.exp(-k * (t - t_in)))
    return c
 
c1 = calc_conc(k0_1, k, vd, T1, t)
c2 = calc_conc(k0_2, k, vd, T2, t)
 
plt.subplot(1, 2, 2)
plt.plot(t, c1, color='blue', label='点滴時間:'+str(T1)+'hr')
plt.plot(t, c2, color='red', label='点滴時間:'+str(T2)+'hr')
# 軸ラベルを表示
plt.ylabel('血中濃度[μg/mL]')
plt.xlabel('時間[hr]')
# 軸の範囲と目盛りを指定する
plt.xlim(0, 12)
plt.ylim(0, 8)
plt.yticks(np.arange(0, 8, 1))
# グリッドの表示
plt.grid(linestyle='dashed')
# ラベルに応じた凡例を表示
plt.legend()
plt.show()