ネットで蓄積率を検索すると『投与間隔/消失半減期が3以下なら定常状態のある薬、4以上なら定常状態のない薬』などの記事が見つかります。今回はこの3や4という数字の意味について見ていきたいと思います。
蓄積率とは
ka>>keという条件下の1-コンパートメント経口投与モデル繰り返し投与において、単回投与時のCmaxと定常状態時のCmaxの比をRとすると次のように表すことができます。
このRを蓄積率といい、この値は「定常状態のC(max)は単回投与時のC(max)の何倍になるか」を知る目安となります。
蓄積率の式をグラフでみる
keではイメージがつかみにくいので、もう少し式を整理します。なので、これを式のkeに代入すると、
見にくくなるのでeの表記をexpに変えています。この式は投与間隔と半減期
のみからなる関数となっています。つまり、このモデルにおいては、定常状態における最高血中濃度が単回投与時の何倍になるかは、投与間隔と半減期のみで決定される、ということを意味しています。
ではこの式を縦軸に蓄積率(R)、横軸に投与間隔/半減期()を取ってプロットしてみます。
import numpy as np import matplotlib.pyplot as plt # 投与間隔/半減期と蓄積率の関係 # 蓄積率を返す def ac_rate(x): return 1 / (1 - np.exp(-np.log(2) * x)) x = np.arange(0.1, 11, 0.1) plt.plot(x, ac_rate(x), label=r"$R = 1/(1-exp(-log2 * τ/t_{1/2})) $") plt.title("$τ/t_{1/2}$とRの関係") # 軸ラベルを表示 plt.xlabel('投与間隔/半減期($τ/t_{1/2}$)') plt.ylabel('蓄積率(R)') # 軸の範囲と目盛り間隔を指定 plt.xlim(0, 10.5) plt.xticks(np.arange(0, x[-1], 1)) plt.ylim(0, 8.5) # 横軸が3, 4の位置に点線を入れる plt.vlines(3, 0, ac_rate(3), color='red', linestyles='dashed') plt.vlines(4, 0, ac_rate(4), color='red', linestyles='dashed') # 矢印とテキストを入れる plt.annotate('', xy=(2.2, 0.4), xytext=(2.9, 0.4), arrowprops=dict(fc='red', shrink=0.08, alpha=0.7)) plt.text(0.4, 0.3, '定常状態あり') plt.annotate('', xy=(4.8, 0.4), xytext=(4.1, 0.4), arrowprops=dict(fc='red', shrink=0.08, alpha=0.7)) plt.text(4.9, 0.3, '定常状態なし') # グリッドの表示 plt.grid(linestyle='dashed', linewidth=0.5) # ラベルに応じた凡例を表示 plt.legend() plt.show()
横軸の取る範囲ですが、投与間隔τは6~24、半減期は2~百数十時間程度として取りあえず0.1~11でプロットしてみました。もちろん、実際の薬の中にはこの範囲に入らないものもあると思います。
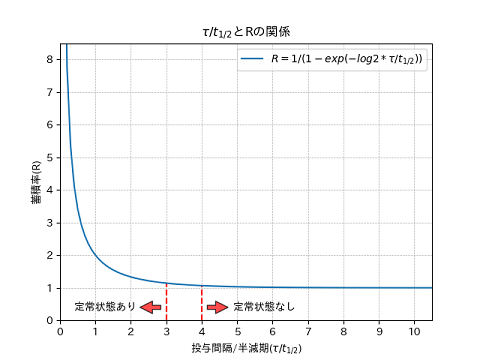
グラフを見てみると、横軸のだいたい3~4あたりを境として投与間隔/半減期が大きくなれば蓄積率Rはほぼ1となり、小さくなればRは1より大きくなっていくのが見て取れます。ちなみに、投与間隔/半減期が3と4のときのRを表示させてみると、次のような値になります。
print(ac_rate(3)) # 1.1428571428571428 print(ac_rate(4)) # 1.0666666666666667
具体的な例で見てみる
取り上げる薬がこのモデル(1-コンパートメント経口投与モデル)に従うという前提での話になりますが、いくつかの薬のとRの値をグラフ上にプロットしてみたいと思います。半減期については、一応インタビューフォームの値を参考にしていますが、厳密なものではありません。
次のコードを、上のコードのx = np.arange(0.1, 11, 0.1)とplt.plot()の間に貼り付けてください。
# key: 薬物名と用法, value: (投与間隔, 半減期) med_dict = {'ロキソプロフェン 1日3回': (8, 1.2), 'ゾニサミド 1日1回': (24, 60), 'ゾニサミド 1日2回': (12, 60), 'アムロジピン 1日1回': (24, 33)} for name, val in med_dict.items(): r = val[0] / val[1] R = ac_rate(r) plt.scatter(r, R) plt.text(r + 0.2, R + 0.1, name) print('{}: 投与間隔/半減期={:.2f}, R={:.2f}'.format(name, round(r, 2), round(R, 2)))
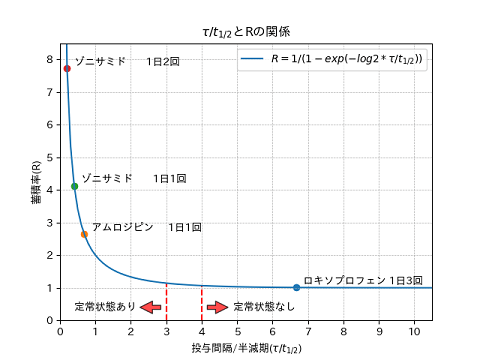
ロキソプロフェン 1日3回: 投与間隔/半減期=6.67, R=1.01 アムロジピン 1日1回: 投与間隔/半減期=0.69, R=2.64 ゾニサミド 1日1回: 投与間隔/半減期=0.40, R=4.13 ゾニサミド 1日2回: 投与間隔/半減期=0.20, R=7.73
ロキソプロフェンのは4より大きく、Rも1と蓄積性はありません。この投与間隔と半減期では繰り返し服用しても、血中濃度は単回服用時とほぼ同じということです。また、添付文書にも『1日3回5日間連続経口投与した場合、いずれも1回投与時と大きな差異はなく、蓄積性は認められていない。』と記載されています。
アムロジピンを見てみるとRは2.64で、インタビューフォームによると2.5mgを1日1回連続投与した場合は『投与後6~8日目に定常状態(初回投与時の約3倍)に達し、以後の蓄積は認められなかった。』とのこと。
ゾニサミドのように服用回数が『1〜3回に分割経口投与』となっているものもあります。その場合は同じ薬でも、当然服用回数によってRは変わってきます。
matplotlibで3Dプロットする
上では蓄積率Rを投与間隔/半減期の関数として平面にプロットしましたが、今度は投与間隔と半減期をそのまま1つの軸に取り、2変数関数として3次元空間にプロットしてみました。
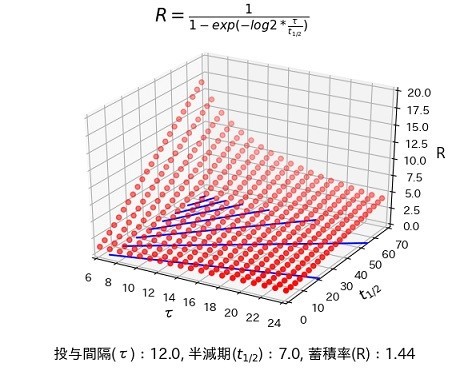
このプログラムではグラフ中の赤い点をクリックすると座標(投与間隔、半減期、蓄積率)をグラフ下に表示することができます。
3Dプロットといっても曲面やワイヤーフレームによる描画などいろいろありますが、今回は散布図にしています。
import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = fig.add_subplot(111, projection='3d') tau = np.arange(6, 25, 1) # 投与間隔 t_half = np.arange(1, 70, 3) # 半減期 tau, t_half = np.meshgrid(tau, t_half) # 格子点を作る R = 1 / (1 - np.exp(-np.log(2) / t_half * tau))
ほぼお手本通りのコードですが、3Dプロット用のモジュールをインポートすること、
fig.add_subplot()にprojection = '3d'を設定すること、が平面プロットと違う点です。また、2次元格子点を作成するためにnp.meshgrid()を使用しています。
これによりtau, t_halfの同じインデックスの値がxy平面上のある一点の座標を示すことになります。
3Dプロットについては、こちらのサイトを参考にしました。
[Matplotlib] 3D (3次元) プロット
次はイベント処理(クリックで座標を表示する)です。関係のある部分だけ抜き出しています。
fig = plt.figure() def on_pick(event): # 何らかの処理 fig.canvas.mpl_connect('pick_event', on_pick)
これについては、Event handling and picking — Matplotlib 3.3.3 documentationのサンプルコードを参考に書きました。
fig.canvas.mpl_connect('pick_event', on_pick)でイベント名とコールバック関数(on_pick)を紐づけておけば、”オブジェクトが選択された”、”マウスボタンが押された”、などのイベントを捕捉し、コールバック関数に書いておいた処理が実行される、ということのようです。
また、on_pick()内の座標の取得部分のコードについては、こちらのサイトを参考にしました。
python - matplotlibの3Dグラフ上の座標を得る - スタック・オーバーフロー
参考
- 徹底解説 薬物動態の数学―微積分と対数、非線形
最後に、今回のコードを載せておきます。
import numpy as np import matplotlib.pyplot as plt # 投与間隔/半減期と蓄積率の関係 # 蓄積率を返す def ac_rate(x): return 1 / (1 - np.exp(-np.log(2) * x)) print('投与間隔/半減期=3のときのR: ', ac_rate(3)) # 1.1428571428571428 print('投与間隔/半減期=4のときのR: ', ac_rate(4)) # 1.0666666666666667 x = np.arange(0.1, 11, 0.1) # key: 薬物名と用法, value: (投与間隔, 半減期) med_dict = {'ロキソプロフェン 1日3回': (8, 1.2), 'アムロジピン 1日1回': (24, 35), 'ゾニサミド 1日1回': (24, 60), 'ゾニサミド 1日2回': (12, 60)} for name, val in med_dict.items(): r = val[0] / val[1] R = ac_rate(r) plt.scatter(r, R) plt.text(r + 0.2, R + 0.1, name) print('{}: 投与間隔/半減期={:.2f}, R={:.2f}'.format(name, round(r, 2), round(R, 2))) plt.plot(x, ac_rate(x), label="$R = 1/(1-exp(-log2 * τ/t_{1/2})) $") plt.title("$τ/t_{1/2}$とRの関係") # 軸ラベルを表示 plt.xlabel('投与間隔/半減期($τ/t_{1/2}$)') plt.ylabel('蓄積率(R)') # 軸の範囲と目盛り間隔を指定 plt.xlim(0, 10.5) plt.xticks(np.arange(0, x[-1], 1)) plt.ylim(0, 8.5) # 横軸が3の位置に点線, 左矢印とテキストを入れる plt.vlines(3, 0, ac_rate(3), color='red', linestyles='dashed') plt.annotate('', xy=(2.2, 0.4), xytext=(2.9, 0.4), arrowprops=dict(fc='red', shrink=0.08, alpha=0.7)) plt.text(0.4, 0.3, '定常状態あり') # 横軸が4の位置に点線, 右矢印とテキストを入れる plt.vlines(4, 0, ac_rate(4), color='red', linestyles='dashed') plt.annotate('', xy=(4.8, 0.4), xytext=(4.1, 0.4), arrowprops=dict(fc='red', shrink=0.08, alpha=0.7)) plt.text(4.9, 0.3, '定常状態なし') # グリッドの表示 plt.grid(linestyle='dashed', linewidth=0.5) # ラベルに応じた凡例を表示 plt.legend() plt.show()
こちらは3Dプロットのコードです。
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D # 蓄積率の式を3Dプロットする # グラフをクリックしたときに呼ばれる関数. 座標をfig上に表示する def on_pick(event): ind = event.ind[0] x, y, z = event.artist._offsets3d label = '投与間隔(τ):{}, 半減期($t_{{1/2}}$):{}, 蓄積率(R):{}'.format(x[ind], y[ind], round(z[ind], 2)) text.set_text(label) text.set_visible(True) fig.canvas.draw_idle() fig = plt.figure() fig.subplots_adjust(top=0.9, bottom=0.15) # 余白の調整 ax = fig.add_subplot(111, projection='3d') # (行,列,番号), projection='3d'でAxes3Dオブジェクトを作成 fig.suptitle(r"$R = \frac{1}{1-exp(-log2*\frac{τ}{t_{1/2}})} $", size=16) # figにタイトルを入れる tau = np.arange(6, 25, 1) # 投与間隔 t_half = np.arange(1, 70, 3) # 半減期 tau, t_half = np.meshgrid(tau, t_half) # 格子点を作る R = 1 / (1 - np.exp(-np.log(2) / t_half * tau)) # 軸ラベルを設定 ax.set_xlabel('τ', size=13) ax.set_ylabel('$t_{1/2}$', size=13) ax.set_zlabel('R', size=13) # 軸の表示範囲を設定 ax.set_ylim(0, 70) ax.set_xlim(6, 24) ax.set_zlim(0, 20) # 3次元散布図を作成. picker:設定することでオブジェクトを選択できるようになる ax.scatter(tau, t_half, R, c='red', picker=True) # 底面に等高線を描画 ax.contour(tau, t_half, R, colors="blue", offset=-1) # テキストをfigに設定 text = fig.text(0.15, 0.05, '', size=13) fig.canvas.mpl_connect('pick_event', on_pick) plt.show()
